ÚLOHY S ANTISIGNÁLEM VE 2. TŘÍDĚ
Autor: Martin Krynický, Gymnázium, Třeboň, Na Sadech 308
Když přicházejí děti na druhý stupeň jejich strategie řešení slovních úloh se nacházejí někde mezi dvěma extrémy:
- „Strategie klíčových slov“: dítě hledá v zadání čísla a klíčová slova (méně, více, krát, …), která vedou k sestavení výpočtů, ze kterých získá výsledek.
- „Strategie modelu popsané situace“: dítě si představí situaci, která je v zadání popsána, v závislosti na situaci najde její matematický model (výpočet) a do něj pak hledá čísla v zadání.
Řešení konkrétní úlohy od konkrétního dítěte samozřejmě často osciluje mezi těmito extrémy. Z pohledu výuky v dalších ročnících je strategie klíčových slov značně problematická. Přestože umožňuje velmi rychle a poměrně spolehlivě řešit typické úlohy, v situacích, které jsou netradiční nebo nové, velmi často zcela selhává (a není divu, když podstatou této strategie je snaha obejít se bez představy o tom, co příklad popisuje) a žáci, jejichž strategie řešení jsou používání klíčových slov nejbližší mají velmi často problémy nejen s řešením slovních úloh, ale matematikou obecně.
Protože strategie klíčových slov je velmi nenáročná na přemýšlení (a vyhovuje tedy přirozené lidské snaze šetřit si práci) tíhnou k ní často i žáci, kteří k ní nejsou ve škole vedeni.
Jedním ze způsobů, jak tento nepříznivý stav změnit by mohlo být častější používání slovních úloh, které se strategii klíčových slov vzpírají:
- Úlohy s antisignálem: úlohy, které obsahují klíčové slovo (například méně) ale ke správnému vyřešení příkladu je nutné použít jiný početní postup než ten, který je se slovem většinou spojován (v případě slova méně tedy sčítat, místo typického odčítání).
- Úlohy nedozadané: úlohy, které neobsahují všechny číselné údaje, které jsou nutné k jejich vyřešení. Řešitel si tedy musí ujasnit, jaká informace mu chybí
- Úlohy obsahující nepotřebné údaje: úlohy, v jejichž zadání se vyskytují i čísla, která nejsou potřebná k jejich vyřešení.
- Úlohy nesmyslné: úlohy, které obsahují údaje, které neumožňují vypočítat řešení, na které se zadání úlohy táže.
Protože cílem sbírky bylo prezentovat různé přístupy k řešení slovních úloh prostřednictvím žákovských řešení, obrátil jsem se na kolegyni Alenu Kučerovou učící na prvním stupni, která byla ochotná mnou navržené úlohy v mojí přítomnosti ve své třídě zadat a nechat je žáky vyřešit. Jednalo se o žáky 2. třídy jedné z třeboňských základních škol, kteří se zatím s žádným z uvedených typů slovních úloh nesetkali. Jejich výuka probíhá podle učebnic a pracovních sešitů nakladatelství Prodos.
Na první z těchto hodin jsem připravil sadu šesti slovních úloh prvních dvou typů. Žáci dostali úlohy na pracovním listu, který obsahoval zadání úloh, volné místo na libovolný postup řešení a linku na odpověď. S kolegyní jsem zkonzultoval srozumitelnost úloh, velikost používaných čísel. Byl jsem dopředu upozorněn, že na dlouhou samostatnou práci děti nejsou zvyklé. Děti na úlohách pracovaly přibližně 30 minut (10 minut zabral běžný úvod hodiny, pět minut před koncem jsme práci ukončili a zkusili vyvolat diskusi o některých příkladech).
Již během hodiny se ukázalo, že mé představy byly silně nadsazené. Většina dětí sice vydržela na úlohách pracovat po celou dobu, ale byly znatelně unavené a jejich výkon citelně klesal. Ačkoliv byly děti dopředu upozorněny na netradičnost úkolů, velká většina třídy řešila většinu úkolů špatně a ani zpětný rozbor jejich řešení nedával mnoho záchytných bodů k společnému rozboru. Navíc se ukázalo, že je nutné dětem zakázat použití gumovacích per, protože téměř všichni nechávali na papíru poslední variantu výpočtu a z odevzdaných pracovních listů se tak ztratila část jejich úvah. Velmi vysoká neúspěšnost řešení první sady příkladů vedla k tomu, že jsem se rozhodl nehonit více zajíců najednou a v dalších hodinách se soustředit pouze na úlohy s antisignálem. Dále rozebírám z úvodní sady úloh pouze tyto dvě. Ukázky řešení jsou neupravované fotografie žákovských prací, které ilustrují text uvedený nad nimi. Pokud cituji řešení v textu uvádím v uvozovkách znění tak, jak bylo napsáno žákem, tedy včetně pravopisných chyb.
Úloha 2: Janička měla letos na narozeninovém dortu 7 svíček, o 28 méně než její maminka. Kolikáté narozeniny maminka letos oslavila?
Řešení | Počet žáků |
| 7+28=35 | 4 |
| 28-7=21 | 12 |
Pouze odpověď: “Letos mamince bilo 19 let.” | 1 |
Nic | 1 |
Tabulka 1 – Přehled žákovských řešení úlohy 2 z první sady úloh
Kromě výpočtu a odpovědi pracovní listy nic dalšího neobsahovaly. Na žádném z pracovních listů se neobjevil výpočet , který by nejpřesněji odpovídal typickému řešení příkladu se signálem méně (od prvního čísla odečítáme druhé), žáci zřejmě automaticky píší rozdíl větší číslo – menší číslo.
Je zajímavé, že nikdo z žáků si zadání příkladu nespojil se skutečností – když jsme se žáků ptali, kolik je jejich maminkám, všichni potvrzovali věk přes třicet let. Skutečnost, že u stejně starého dítěte v příkladu by maminka měla pouze 21 let, nikoho z nich nezarazila.
Zajímavou informaci o síle antisignálu jsme získali v příkladu 4. Do třídy jsme jej zadali ve dvou variantách (skupiny představovaly dvě oddělení třídy, v každé ze skupin byli dva žáci, kteří správně vyřešili úlohu 2). Žáci byli během práce na příkladu vyzváni k tomu, aby si řešení usnadnili obrázkem.
Úloha 4 (Verze 1): Petrovi trvá cesta do školy 17 minut. Je to o 8 minut méně, než na cestě stráví Eliška. Jak dlouho cestuje do školy Eliška?
Všichni žáci s tímto zadáním příklad řešili špatně výpočtem . Většina z nich si nakreslila obrázek, všechny bez výjimky byly špatně.
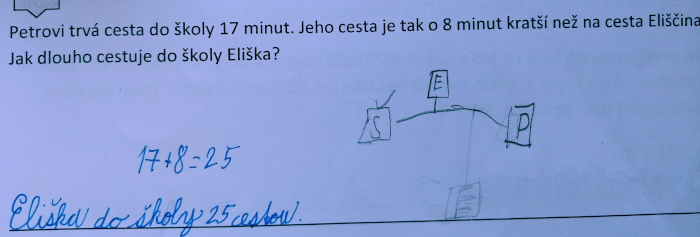
Úloha 4 (Verze 2): Petrovi cesta do školy trvá 17 minut. Jeho cesta je tak o 8 minut kratší než na cesta Eliščina. Jak dlouho cestuje do školy Eliška?
Řešení | Počet žáků |
17-8=9 (bez obrázku nebo špatný obrázek) | 5 |
17+8=25 (špatný obrázek) | 1 |
17+8=25 (dobrý obrázek) | 2 |
17+8=25 (bez obrázku) | 1 |
Odpověď: 11 min (bez výpočty i obrázku) | 1 |
Tabulka 2 – Přehled žákovských řešení úlohy 4 z první sady úloh
Z výsledků je zřejmé, že pokud se v zadání použije slovo kratší, je antisignál daleko slabší a žáky méně svádí ke špatnému výsledku. Druhá věc, která je zřejmá, že žáci obrázek kreslí až ve chvíli, kdy jsou v podstatě rozhodnutí o tom, jaký výpočet udělají a jeho nakreslení na pokyn učitele nezvyšuje jejich šance na správné řešení.
Průběh druhé vyučovací hodiny
Nejdříve byly ve třídě zadány pracovním listu dvě slovní úlohy. Pracovní list obsahoval na jedné straně pouze zadání obou úloh, vynechané místo na práci žáků a linku na odpověď. Žáci řešili obě úlohy samostatně. Poté co velká většina žáků vyřešila obě úlohy následovala diskuse se třídou.
Úloha 1: Jirka chodí teprve do druhé třídy, ale přesto pomáhá tatínkovi na stavbě. Dneska nosili cihly do patra, Jirka unesl najednou tři, což je o čtyři méně, než najednou unesl tatínek. Kolik cihel unese nejednou tatínek?
Řešení | Počet žáků |
| 4+3=7 | 12 |
4-3=1 opraveno na 4+3=7 | 2 |
3+4=7 | 1 |
3+3=6 | 1 |
| 2+3+4=9 | 1 |
Prázdný papír. | 1 |
Tabulka 3 – Přehled žákovských řešení úlohy 1 z druhé sady úloh
Z výsledků je vidět, že žáci se antisignálem splést nedali. I obě řešení žáků, kteří měli problém v zadání úlohy nalézt číselné údaje, jsou založeny na sčítání a vedou k výsledku většímu než 4. Dva žáci příklad nejdříve vyřešili chybně (odčítáním), ale poté svůj výsledek opravili tak, aby byl počet cihel, které unese tatínek větší, než kolik jich unese Jirka.
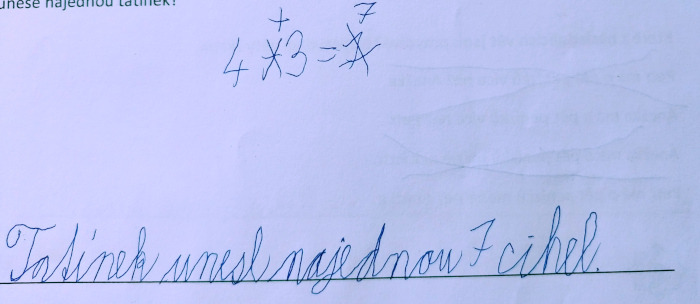
Obrázek 2 – Ukázka žákovského řešení (archiv autora)
Při kontrole jsme se nejdříve zeptali na výsledky. Každý navržený výsledek jsme napsali na tabuli, snažili jsme se postupovat tak, aby nebylo příliš zřejmé, kolik a kterých žáků navrhuje každou z variant. Bohužel se ani jednou neobjevil typický antisignální výsledek 1 (z výpočtu ) a tak jsme se nemohli nikoho zeptat, jak k tomuto výsledku dotyčný žák došel. Zeptali jsme se tedy žáků, kteří špatný výsledek 1 ještě během řešení opravili na správný 7. Dozvěděli jsme se, že v zadání je o čtyři méně a mělo by se tedy odečítat, ale 1 je určitě špatný výsledek, protože tatínek určitě unese víc než 1 cihlu. Zbývající špatné výsledky (vyplývající ze špatné identifikace relevantních čísel v zadání) jsme s celou třídou nerozebírali. Dobře řešící žáci pak opakovali, že tatínek musí unést víc cihel než Jirka, a proto se musí při řešení úlohy sčítat i když je v ní uvedeno „odčítací“ slovo „méně.
Úloha 2: V supermarketu stojí kilo banánů 34 Kč, což je o 7 Kč méně než v místním obchodě. Kolik stojí kilo banánů v místním obchodě?
Řešení | Počet žáků |
| 34+7=41 | 3 |
| 34-7=27 | 10 |
34+7=41 | 1 |
| 34+7=27 | 1 |
| 34-7=19 | 1 |
Prázdný papír. | 2 |
Tabulka 3 – Přehled žákovských řešení úlohy 2 z druhé sady úloh
Přesně opačná situace než u předchozího příkladu. Zajímavé jsou třetí a čtvrté řešení, kdy žák zřejmě správně odhalil, že by se mělo sčítat, ale očekával menší výsledek, ke kterému nakonec v obou případech došel.
Už během práce žáků na samostatném řešení obou příkladů bylo jasné, že u druhého z nich je úspěšnost daleko menší. Stejně jako u prvního příkladu jsme na tabuli nejdříve napsali všechna nabízená řešení, tentokrát jsme k řešením psali i postupy. Jako první svůj výsledek obhajovali ti, kteří příklad řešili špatně (postup ). Jako důvod k použití odčítání uváděli slova méně v zadání (stejné slovo, které při řešení prvního příkladu na výběr početní operace vliv nemělo), které znamená, že při řešení musíme odečítat. Obhájci správného řešení tvrdili (správně), že v zadání je sice méně, ale méně znamená, že jsou levnější v supermarketu a v místním obchodě tedy musí stát více a při výpočtu větší ceny se musí sčítat. Touto argumentací však téměř nikoho ze skupiny špatně řešících žáků nepřesvědčili. Během této diskuse se k překvapení obou přítomných učitelů zjistilo, že jen velmi malá část dětí zná význam slova supermarket. Ani poté, co jsme si vysvětlili, že se jedná o velký obchod s nabídkou potravin (v Třeboni je nejznámějším příkladem místní Kaufland), děti nechápaly, proč by ve velkém obchodě měly být banány levnější. Následovalo tedy ještě krátké povídání o tom, proč rodiče jezdí na velké nákupy právě do místního Kauflandu, co to jsou slevy, a jaké nevýhody má malý místní obchod proti supermarketu z velkého mezinárodního řetězce. Teprve poté se začala většina původně špatně řešících dětí přiklánět ke správnému řešení. Dokonce se objevil postřeh, že je to vlastně stejné jako u prvního příkladu, protože v místním obchodě stojí banány víc, stejně jako musí táta unést víc než Jirka.
V další části hodiny (kterou jsme začali se zpožděním kvůli diskusi o supermarketech) žáci nejprve samostatně pracovali na dalších dvou úlohách. Zadání příkladu 3 obsahovala dva obdélníčky se jmény děti, pro nakreslení obrázků s počtem penízků. Pod zadáním příkladu 4 byla úsečka s křížkem označeným písmenem T a dalšími dvěma nepopsanými křížky (Stráž a Lásenice jsou dvě velké vesnice ležící na hlavní silnici z Třeboně do okresního města Jindřichův Hradec, navíc během samostatné práce jsme nechali na tabuli promítat mapu cesty).
Samostatnou práci žáků na úkolech jsme ukončili asi pět minut před koncem hodiny, takže většina žáků nestihla dokončit příklad 4. Kontrolu jsme prováděli hlasováním: žáci buď zvedli palec nahoru (věta je pravdivá) nebo ukázali palcem dolů (věta je nepravdivá). Hlasování se účastnili i žáci, kteří nestihli vyškrtat odpovědi na papírech.
Úloha 3: Anežka našla při hře třináct penízků, Petr jich našel jenom osm. Do vyznačených políček můžeš nakreslit u každého obrázek s počtem penízků, které Anežka i Petr mají.
Které z následujících vět jsou pravdivé? Nepravdivé škrtni.
- Petr má o pět kartiček více než Anežka.
- Anežka má o pět kartiček více než Petr.
- Anežka má o pět kartiček méně než Petr.
- Petr má o pět kartiček méně než Anežka.
Řešení | Počet žáků |
Všechny odpovědi správné | 14 |
Neškrtnutá odpověď: „Petr má o pět penízků více než Anežka“ | 1 |
Škrtnutá odpověď: „Petr má o pět penízků méně než Anežka“. | 1 |
Prázdný papír. | 2 |
Tabulka 5 – Přehled žákovských řešení úlohy 3 z druhé sady úloh

Obrázek 3 – Ukázka žákovského řešení (archiv autora)
Úloha 4: Cesta z Třeboně do Stráže nad Nežárkou měří 14 km, do Lásenice je to z Třeboně 20 km. Které z následujících vět jsou pravdivé? Nepravdivé škrtni.
- Vzdálenost do Stráže je o 6 km menší než do Lásenice.
- Vzdálenost do Lásenice je o 6 km větší než do Stráže.
- Vzdálenost do Stráže je o 6 km větší než do Lásenice.
- Vzdálenost do Lásenice je o 6 km menší než do Stráže.
Řešení | Počet žáků |
Všechny odpovědi správné | 3 |
Neškrtnutá odpověď: „Vzdálenost do Lásenice je o 6 km menší …“ | 2 |
Obráceně vyhodnocené odpovědi ohledně Lásenice. | 1 |
Škrtnutá odpověď: „Vzdálenost do Lásenice je o 6 km větší …“, neškrtlá odpověď: „Vzdálenost do Stráže je o 6 km větší, …“. | 1 |
Škrtnutá odpověď: „Vzdálenost do Lásenice je o 6 km větší …“. | 1 |
Prázdný papír. | 10 |
Tabulka 6 – Přehled žákovských řešení úlohy 4 z druhé sady úloh
Podle výsledků třetího příkladu na papírech i hlasování u čtvrtého příkladu se zdá, že chyby byly spíše výjimečné.
Na diskusi o závěrečném problému: „Jak souvisí třetí a čtvrtý příklad se slovními úlohami ze začátku hodiny? Proč jsme třetí a čtvrtý příklad dělali?“ téměř žádný čas nezbyl, od dětí padly asi tři nepříliš zajímavé návrhy. Zamýšlený důvod „Z obou příkladů je vidět, že stejný rozdíl v množství je možné vyjádřit vždy dvěma způsoby: Anežka má o 6 více nebo Jirka má o 6 méně. Z toho, že se v zadání vyskytuje samotné slůvko méně, automaticky nevyplývá, že při řešení budeme odečítat. Vždy si musíme rozmyslet, na koho se slůvko méně vztahuje a co to pro výpočty ze zadanými čísly znamená.
Třetí hodina
Třetí sada příkladů byla zadávána bez mé přítomnosti dva dny pro druhé hodině. Pomocí série tří příkladů jsme chtěli ověřit dopad předchozí hodiny.
Úloha 1: Kilo pomerančů strojí 39 Kč. V akci stojí o 10 Kč méně. Kolik stojí kilo pomerančů v akci?
Řešení | Počet žáků |
| 39-10=29 | 12 |
| 39+10=49 | 5 |
| 39-10=11 | 1 |
Prázdný papír. | 1 |
Tabulka 7 – Přehled žákovských řešení úlohy 1 z třetí sady úloh
Cílem příkladu bylo zjistit, zda se část dětí nerozhodne používat signální slova obráceně (tedy zda si z předchozí hodiny neodnese závěr, že méně znamená sčítat). Bohužel nemáme přímé srovnání se signálním příkladem zadaným v první hodině, ale zdá se, že menší část žáků doopravdy jen prohodila význam slova méně a začala při jeho výskytu v zadání sčítat.
Úloha 2: Během dětského dne vyhrál Tonda celkem 36 bonbónů, což je o 6 méně než vyhrál Adam. Kolik bonbónů vyhrál Adam?
Řešení | Počet žáků |
| 36+6=42 | 8 |
| 36-6=30 | 9 |
42-6=36. Adam vyhrál 42 bonbónů. | 1 |
Prázdný papír. | 1 |
Tabulka 8 – Přehled žákovských řešení úlohy 2 z třetí sady úloh
Úloha obsahuje antisignál v nejobtížnější podobě (kontext žákům nenapovídá jako u úlohy s nošením cihel). Téměř polovina žáků ho vyřešila správně (někteří opravili původně špatný výsledek, zajímavé je řešení, které se vyhýbá použití sčítání při zápisu na papír, přesto dochází ke správnému výsledku).
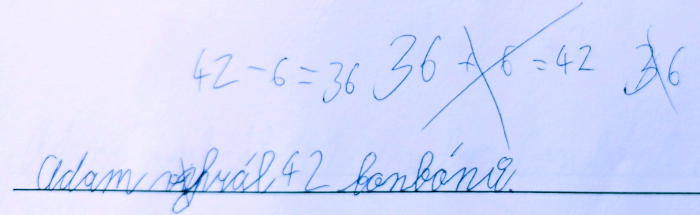
Obrázek 4 – Ukázka žákovského řešení (archiv autora)
Úloha 3: Jirkovi je 12 let, to je o čtyři roky více než je jeho mladší sestře Elišce. Kolik let je Elišce?
Řešení | Počet žáků |
| 12-4=8 | 13 |
| 12-4=9 | 1 |
| 12+4=16 | 3 |
Prázdný papír. | 1 |
Tabulka 9 – Přehled žákovských řešení úlohy 3 z třetí sady úloh
Úloha obsahuje jako antisignál slovo více (všechny předchozí úlohy měly jako antisignál slovo méně) na druhou stranu obsahuje silnou kontextovou nápovědu mladší sestře Elišce. Tato nápověda zřejmě způsobila, že tato úloha má největší úspěšnost ze všech úloh.
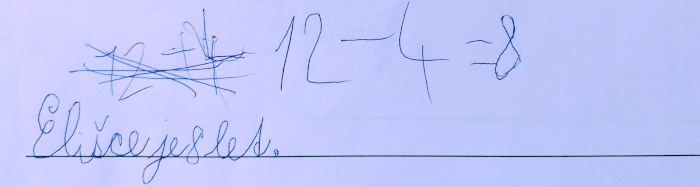
Obrázek 5 – Ukázka žákovského řešení (archiv autora)
I tady však našly případy, kdy signál sčítání ve slově více zvítězil a mladší sestře tak bylo více než staršímu bratrovi.

Obrázek 6 – Ukázka žákovského řešení (archiv autora)
Závěry
Z výše uvedeného se zdá, že:
- I v případě, že strategie klíčových slov není přímo vyučována, velká část dětí si ji samovolně osvojuje, pokud je funkční při řešení úloh, se kterými se setkávají. Používání této strategie je možné omezit tím, že se žáci setkávají s příklady, ve kterých strategie nefunguje.
- Míra, ve které žáci strategii klíčových slov používají závisí na síle signálního slova (méně ovlivňuje jejich postup více než kratší) a kontextu úlohy, který může (pokud je dětem známý) napovídat správné řešení a zeslabovat vliv signálního slova.
- Orientaci v příkladech porovnávajících dvě množství usnadňuje řešení příkladů, které se soustředí na to, že jeden vztah mezi dvěma množstvími je možné vyjádřit jak slovem méně, tak slovem více (podle toho „z které perspektivy se na obě množství díváme“).
Návrhy na použití v hodinách
- Již od druhé třídy by měly být slovní úlohy zadávány střídavě se signálem a antisignálem, aby žáci nezískávali pocit, že strategie slepého následování klíčového slova vede k správnému řešení.
- Významnou pomoc při řešení úloh s antisignálem přináší kontext úlohy, který napovídá správný výsledek i postup.
- Změna v přístupu nepřichází u všech žáků ihned, u některých hrozí „obrácení“ signálního slova (například méně začnou používat pro automatické sčítání).
- Řešení úloh je nutné s žáky neustále rozebírat.
Návrhy na vylepšení zveřejněných příprav:
- Pracovní list se zadanými úlohami by měl mít ještě druhou stranu s prací pro rychlejší část žáků například otázkou: „Zamysli se, jaké špatné výsledky se mohou objevit při řešení slovních úloh na první straně. Proč by mohli jiní žáci tyto chyby udělat?“ nebo zadáním dalších úloh s ještě slabší nápovědou antisignálu.
- Pokud známe třídu, se kterou pracujeme, je třeba využít samostatnou práci třídy na individuální práci s žáky, kteří mají s řešením největší problémy.
Osobní ponaučení
Na prvním stupni je nutné sledovat daleko více věcí a předpokládat jich daleko méně.
