Autor: Pavel Bobek, ZŠ Solidarita

Řešení, respektive reprezentace slovních úloh a problémů pomocí bar models, počeštěně bar modelů, je uplatňováno zejména v singapurské a celkově asijské výuce matematiky a v tamějším mastery modelu výuky, v němž ovládnutí daného konceptu celou třídou je předpokladem a podmínkou postupu třídy k navazující látce. Bar modely stejně jako výuka, kde nedochází ke vzniku velkých rozdílů mezi dovednostmi žáků stejného věku, se v posledních letech etablovaly také ve Velké Británii (viz učební řady Mathematics Mastery, Complete Maths nebo volně dostupná White Rose Maths).

Bar modely jsou užívány napříč všemi stupni výuky matematiky, protože umožňují reprezentovat pomocí jednoduchého instrumentária jak základní (např. sčítání a odčítání přirozených čísel), tak i pokročilejší (rovnice, objem, poměr, zlomky – viz např. zlomková zeď) a pokročilé matematické koncepty (statistika). Svou povahou jsou bar modely spojovníkem mezi konkrétní (spojovatelné kostky, Dienesovy kostky, Cuisenairovy hranoly apod.) i obrazovou reprezentací čísel (náčrtky, tečky aj.). V případě slovních úloh také slouží jako most mezi verbální (text úlohy) a abstraktní reprezentací (výpočet vyjádřený čísly a operacemi) daného problému.

Hlavní předností bar modelů je vyjádření vztahů mezi známými i neznámými hodnotami a navedení žáků k užití vhodné operace pro řešení daného problému. Vyrovnají se konkrétním manipulativům (kostky apod.), avšak k jejich užití stačí obyčejná tužka a papír. Kromě toho je možno s jejich pomocí reprezentovat všechna čísla, tedy i víceciferná čísla a jiná než přirozená čísla. Bar modely naopak neslouží k tomu, aby za žáky provedly samotné výpočty: pokud žák nezná např. algoritmus pro písemné odčítání, bar model mu nepomůže. Mohou však žákům usnadnit kontrolu výpočtů i předběžný odhad výsledku.

V předkládané sekvenci řešili žáci třetí třídy s pomocí bar modelů několik slovních úloh, v nichž se vyskytovaly všechny čtyři základní operace. Sekvence je prezentována v pořadí sčítání – odčítání – násobení – dělení – dělení se zbytkem, tj. tak, aby se komplexita pro čtenáře postupně zvyšovala. V dané hodině však bylo pořadí změněno tak, aby volba operace nebyla předvídatelná.

Úlohy jsou zvoleny tak, aby obsahovaly tyto čtyři operace v jejich čisté formě (s výjimkou dělení se zbytkem, které je rozšířením běžného dělení) a čtenáři ukazovaly jejich reprezentace pomocí bar modelů. Proto se mohou zdát úlohy na první pohled jednoduché, avšak cílem je ukázat metodu samotnou, bez dalších elementů, které by odváděly pozornost od jádra věci. Další gradace úloh je tedy možná a samozřejmě i žádoucí (doplňující otázka, přidání irelevantních údajů, vícekrokové úlohy apod.), avšak není předmětem tohoto příspěvku. Podobně i snížení komplexity připadá v úvahu, ideálně ve formě scaffoldu, tedy “lešení” (například před přípravou neúplného bar modelu, před přípravou zápisu ve formě “víme” / “nevíme” apod.), opět však není předmětem textu.

Postup řešení úloh je pokaždé obdobný:

(1) zápis – zjištění známých a neznámých údajů,

(2) reprezentace údajů a vztahů mezi nimi pomocí bar modelu s popisky včetně popisu neznámé pomocí otazníku nebo prázdného obdélníku (je možno doplnit i slovní popisky, případně nahradit popisky uvnitř obdélníků složenými závorkami vně),

(3) výpočet včetně kontroly výpočtu pomocí užití alternativní operace v bar modelu či odhadu neznámé na základě proporcí bar modelu,

(4) zápis slovní odpovědi.

1) Úloha na sčítání (agregace): Za školní rok 2021/22 získal červený tým 184 bodů, modrý tým získal 237 bodů. Kolik bodů získaly oba týmy dohromady?

Obrázek 1 – Ukázka žákovského řešení (archiv autora)

V této úloze se jedná o nejsnazší formu sčítání – agregaci. Aby žák našel neznámé číslo, musí sečíst dvě hodnoty (počet bodů červeného a modrého týmu). Pomocí zápisu zjistí, že neznámý fakt je právě součet obou známých hodnot. Na základě znalosti modelu celek – část dokáže odvodit, že červený a modrý tým budou patřit do bar modelu vedle sebe (části), zatímco součet (celek) bude reprezentován nejdelším obdélníkem, který obsahuje obě kvantity.

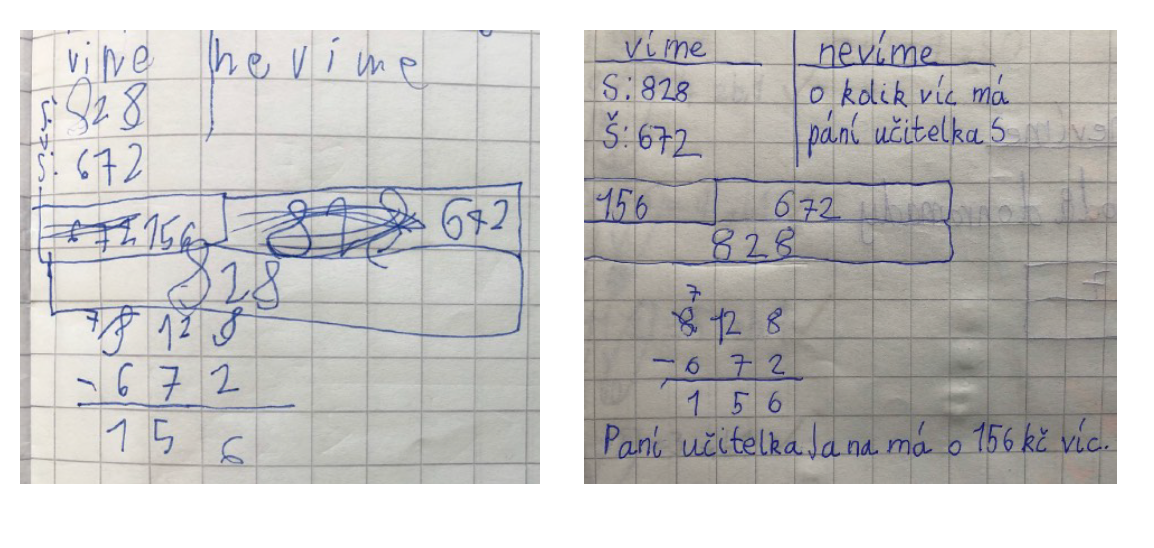
2) Úloha na odčítání (porovnávání čísel): Paní učitelka Schaynová má v peněžence 828 Kč. Paní učitelka Šiftancová má 672 Kč. O kolik korun víc má v peněžence paní učitelka Schaynová?

Obrázek 2 – Ukázka žákovského řešení (archiv autora)

Tato úloha je pro žáky náročnější než jiné úlohy na odčítání proto, že neodebírá z celku. Namísto toho porovnává dvě hodnoty, přičemž se ptá, o kolik větší je ta větší z nich, aniž by zmiňovala slovo rozdíl. Slovo větší mnohé žáky vede k úvaze, že v této úloze budou muset sčítat. Žák s podpůrnými opatřeními (vlevo) proto nejprve zapsal obě známé hodnoty do bar modelu vedle sebe. Na doporučení učitele své rozhodnutí přehodnotil.

Správně zapsal 672 do většího z obou horních obdélníků (část resp. menšitel), menší z nich (část resp. rozdíl) nechal prázdný, 828 zapsal do spodního obdélníku (celek resp. menšenec). Žák vpravo vypracoval úkol zcela samostatně. Oba bez problémů odečetli sloupcovou metodou (“písemné odčítání”). Pro její správné provedení však znalost bar modelu nehraje žádnou roli.

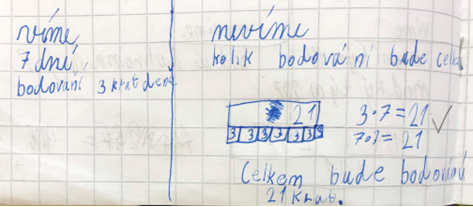
3) Úloha na násobení: 3. C stráví na škole v přírodě přesně týden. Pan učitel boduje pokoje třikrát denně. Kolikrát celkem bude pan učitel bodovat každý pokoj?

Obrázek 3 – Ukázka žákovského řešení (archiv autora)

Výhodou bar modelů je reprezentace pro děti velmi abstraktního násobení v podobě opakovaného sčítání, které je pro žáky srozumitelnější. Žák je tak nucen k přemýšlení nad tím, kolik skupin po kolika členech zobrazuje. Nevýhodou je složitější zápis s větším počtem obdélníků než u sčítání a odčítání. Žákyně, jejíž ukázka je přiložena, nejprve chybně identifikovala číslo 7 (jeden týden = 7 dní) jako celek resp. součin. Pak si uvědomila, že 7 dní je 7 skupin, v rámci nichž došlo pokaždé ke třem bodováním. Číslo 7 škrtla, nakreslila 7 skupin po třech, zapsala výpočet 3 . 7 = 21 i 7 . 3 = 21 (sedm skupin po třech je 21) a doplnila číslo 21 do nejdelšího obdélníku, jehož hodnota je rovna součtu všech malých obdélníků pod ním.

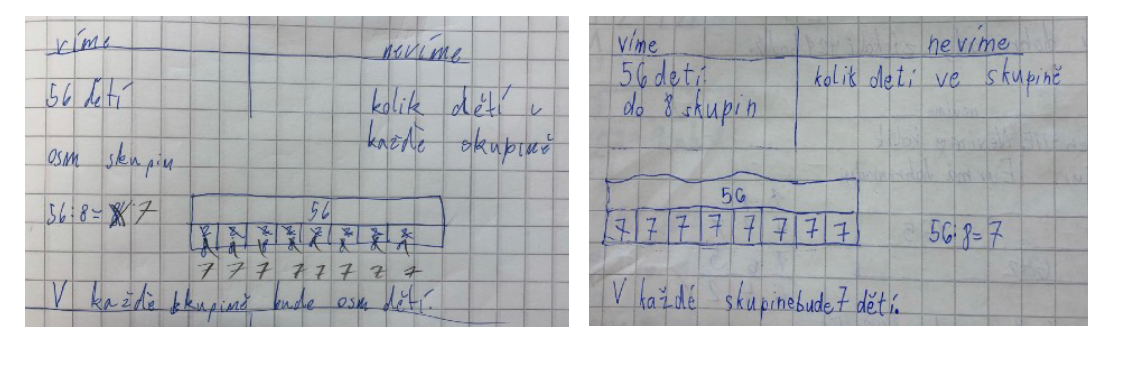
4) Úloha na dělení (dělení do rovných skupin): Na Noc s Andersenem přišlo 56 dětí. Paní učitelky je rozdělily do 8 stejně velkých skupin. Kolik dětí bylo v každé skupině?

Obrázek 4 – Ukázka žákovského řešení (archiv autora)

Při dělení žák nejprve musí identifikovat číslo 56 jako dělence resp. celek a umístit jej do nejdelšího obdélníku. Následně se musí rozhodnout, do kolika skupin bude tento celek dělit.

Žákyně z ukázky vlevo postupovala tak, že nejprve chybně vydělila 56 : 8  = 8. Teprve poté nakreslila bar model, v němž správně rozdělila 56 do osmi skupin, tj. spodní obdélník bar modelu rozdělila do osmi malých obdélníků. Číslo osm poté zapsala do každého z osmi malých obdélníků. V každé skupině jí tedy vyšlo osm dětí. Po společné kontrole ve dvojicích svou práci opravila. Sousedka postupovala tak, že nejprve nakreslila bar model, který ji navedl ke správnému výpočtu (56 : 8 = 7). Při zápisu sedmiček do bar modelu mohla počítat v násobcích sedmi, aby zkontrolovala, zda souhlasí, že osm sedmiček je 56.

Je vhodné žáky motivovat k takového formě kontroly. Neshoda mezi celkem (zde: horní řádek bar modelu) a součtem částí (zde: dolní řádek bar modelu) naznačuje, že při výpočtu došlo k chybě. Bar model sice nedokáže za žáky provést výpočty, ale kromě toho, že je navede ke správné operaci, dokáže žákům na základě obrazové reprezentace naznačit, že ve výpočtu není něco v pořádku (osm osmiček není rovno 56).

5) Úloha na dělení (dělení se zbytkem): Do 4. A chodí 26 žáků. Paní asistentka Jitka je chce rozdělit do tří stejně velkých skupin. Povede se jí to? Pokud ne, kolik žáků bude v každé skupině a kolik jich zbyde?

Obrázek 5 – Ukázka žákovského řešení (archiv autora)

V úloze, kde dělíme se zbytkem, dosahuje zápis pomocí bar modelu zatím nejvyššího stupně komplexity: kromě identických skupin musí žák v řádku částí přidat i díl o odlišné hodnotě (zbytek). Žák z ukázky použil k výpočtu bar model, poté použil standardní abstraktní zápis. Jak je vidět ze zmizíkování v sešitě, původně ve výpočtu chyboval, svůj výpočet však opravil. Je možné se domnívat, že k této opravě výpočtu došlo i na základě bar modelu: součtem částí (zde: spodní řádek) a jeho porovnáním s celkem (zde: horní řádek) lze kontrolu snadno provést. Kontrola přes abstraktní zápis pomocí inverzní operace (8 . 3 = 24) a přičtení zbytku (24 + 2 = 26) je podstatně komplikovanější a náchylnější k chybám.

Literatura a další odkazy:

Mackle, K. (2020). Thinking Deeply about Primary Mathematics. Woodbridge: John Catt Educational.

The Bar Model: A representation used to expose mathematical structure. National Centre for Excellence in the Teaching of Mathematics, https://www.ncetm.org.uk/classroom-resources/ca-the-bar-model/ (zobrazeno 1.6.2022)

The Ultimate Guide To The Bar Model: How To Teach It And Use It In KS1 And KS2. Third Space Learning, https://thirdspacelearning.com/blog/teach-bar-model-method-arithmetic-maths-word-problems-ks1-ks2/ (zobrazeno 14.6.2022)

White Rose Maths, https://whiterosemaths.com/resources?year=year-1 (zobrazeno 24.6.2022)