DRAMATIZACE, JEDEN Z NÁSTROJŮ ŘEŠENÍ SLOVNÍCH ÚLOH
Autoři: Darina Jirotková, Sylva Peclinovská
Proč dramatizace?
Slovní úlohy (1) jsou obecně považovány za obtížnou a velmi často za neoblíbenou součást výuky matematiky. Příčinami obtíží, proč se žákům nedaří řešit slovní úlohy, tedy úlohy, které se snaží zachytit reálné situace, se zabývá např. publikace (2) Kritická místa matematiky na základní škole očima učitelů (Rendl, Vondrová, 2013, s. 96-107).
Jednou z možných cest, jak můžeme jako učitelé žákům pomoci zlepšovat se v porozumění slovním úlohám a ve schopnostech je řešit, je nabízet jim širokou paletu různých řešitelských strategií (3), tedy způsobů, jak je možné slovní úlohy uchopit a řešit.
Příklady různých strategií řešení slovních úloh
Následující strategie je vhodné, dokonce velice žádoucí, aby je žáci používali již, a především, od mladšího školního věku:
Jedním ze způsobů, které mohou pomoci žákovi úlohu pochopit, je s použitím jednoduché pomůcky, jako například různá manipulativa (víčka, fazole, kaštany, knoflíky, …) si situaci úlohy modelovat a řešit pomocí manipulace s těmito předměty.

Obr. 1. Modelace situace (foto autor)
Velice častým způsobem uchopování úlohy je zakreslování situace a řešení pomocí obrázku.
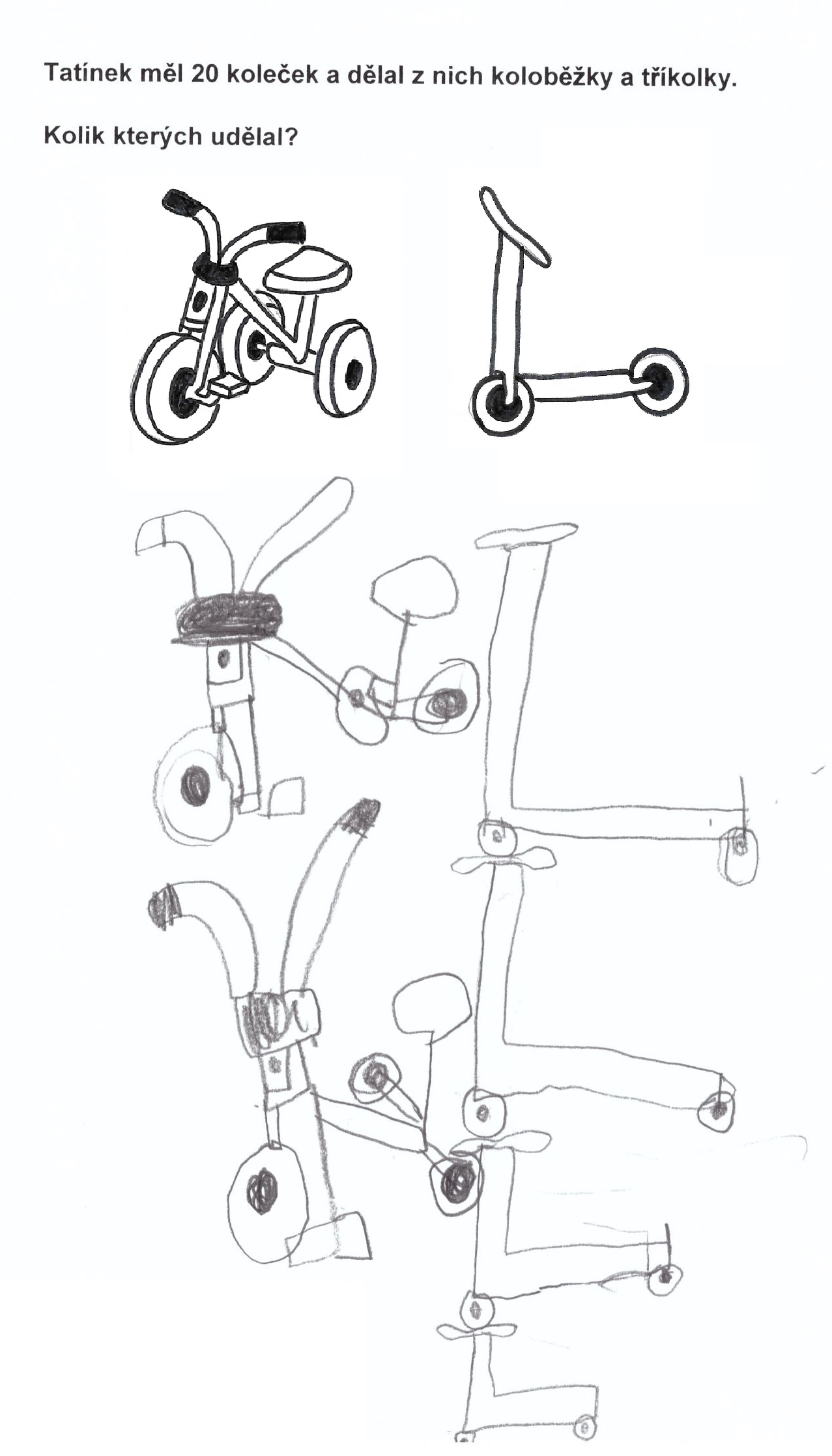
Obr. 2. Řešení vizualizací (archiv autora)
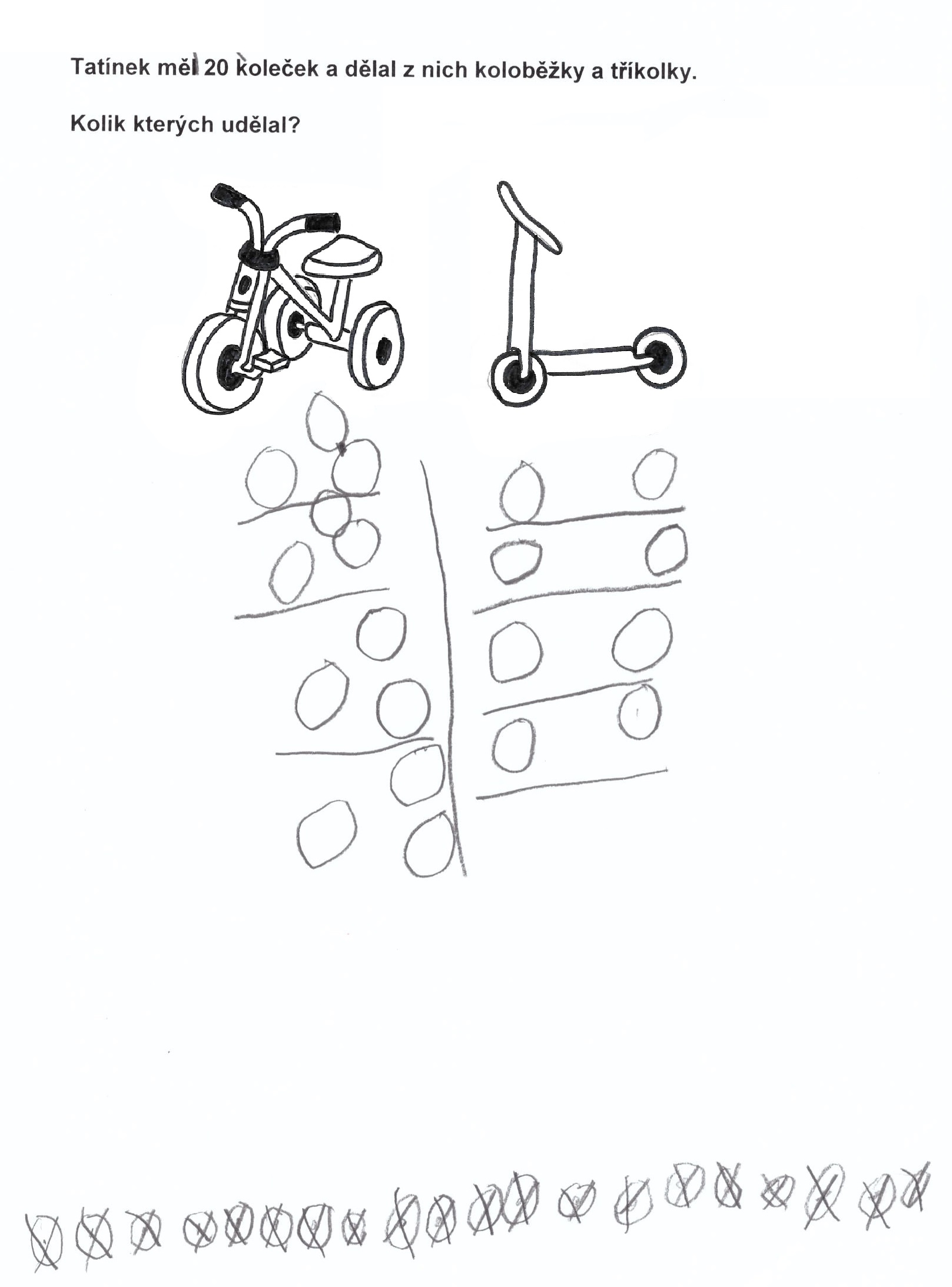
Obr. 3. Řešení strukturovanou vizualizací (archiv autora)
U řešení na obrázku 2 vidíme potřebu dítěte zachytit reálnou podobu tříkolek a koloběžek, zatímco žák vpravo již abstrahoval od podoby tříkolek a koloběžek a zachytil jen podstatné jevy – počet koleček.
Méně častou, avšak velice významnou pomocí při tvorbě představ o situaci úlohy může být sehrání jejího děje. Žák tak situaci úlohy prožívá vlastním tělem a pohybem a takový fyzický zážitek zanechá v paměti hlubokou paměťovou stopu. Tím se vytvoří kvalitní podklad pro porozumění a nalezení řešení. Této strategii se podrobně věnujeme v následující části.
STRUKTURÁLNÍ STRATEGIE (matematický model) (7)
Strukturální strategie řešení slovních úloh lze považovat za nejpokročilejší, protože žák si již umí vytvořit situační model pouze v mysli a nepotřebuje vizuální oporu. Je již schopen zapsat vztahy v úloze jen pomocí čísel a další symboliky a početních operací. U této strategie je však výrazné nebezpečí, že se žák naučí, jak úlohu zapsat, ale skutečně tomu nerozumí, a tak může vzniknout formální poznání. Učitel by měl vždy ověřit, zda skutečně žák úloze rozumí natolik, že si již nic nepotřebuje zobrazit, nebo zda má způsob řešení naučený, či jen tipuje, která čísla a jakou početní operací spolu propojí. (10)
Žák A. – Správně přiřazuje operaci dělení procesu rozdělování koleček na tříkolky či koloběžky. Dále se však žákyně dostala do “zajetí” čísel a již si nebyla vědoma, co počítá.

Obr. 4. Žák A – řešení slovní úlohy strukturálně
Žák B. Není evidence o tom, jakým způsobem žák přišel na řešení. Pravděpodobně první řešení našel vhledem a od něj odvozoval další. Uspořádání výsledků do tabulky má velký potenciál pro to, aby našel všechna řešení.

Obr. 5. Žák B – řešení slovní úlohy
Žák C. Je zřejmé, že prvním pokusem, který je škrtnut, žák získal vhled. Na druhý pokus již určil jeden výsledek.

Obr. 6. Žák C – řešení slovní úlohy strukturálně
Žák D. Žák zachycuje proces, jak postupně odebírá kolečka střídavě na koloběžky a pak na tříkolky.
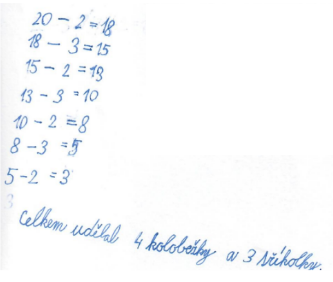
Obr. 7. Žák D – řešení slovní úlohy strukturálně
———————————————————————————————————————–
Naším cílem je věnovat pozornost řešitelské strategii, která ve škole sice není běžně využívaná, avšak pro porozumění některým slovním úlohám je pro žáky především mladšího školního věku klíčová. Tato strategie se obvykle označuje jako DRAMATIZACE, někdy též sehrávka. Tím rozumíme sehrání situace úlohy tak, že žáci jsou hlavními aktéry.
Strategie dramatizace je účelná především v úlohách, kde hraje významnou roli čas a jeho plynutí. Tyto úlohy nazýváme dynamické (8). Jistě si vzpomeneme např. na úlohy o pohybu. V rámci prvního stupně základní školy se s těmito úlohami běžně nepracuje, ale o to více pak tyto úlohy dělají problémy žákům na druhém stupni. Domníváme se, že zařazení dynamických úloh již na 1. stupni ZŠ je důležité, avšak musí být přiměřené věku a úrovni žáka. Proto zde nabízíme tzv. slovní úlohy o věku. Jsou jak dynamické, děj probíhá v čase, tak zároveň jsou postavené na reálném kontextu, který je blízký zkušenostem žáků. A právě pro porozumění a řešení těchto úloh je dramatizace ideálním nástrojem.
Nelze se však spoléhat na to, že tato řešitelská strategie je vhodná pro všechny úlohy a pro všechny žáky. Jak bylo řečeno již dříve, ideální je, když se žák seznámí s různými řešitelskými strategiemi, z nichž si pak při řešení dané úlohy může volit pro sebe tu nejvhodnější.
2. Slovní úlohy o věku
Slovní úlohy o věku jsou slovní úlohy, jejichž reálný kontext se týká věku osob nebo nějakých bytostí. Jsou náročné tím, že věk, např. 7 let, je veličina, kterou nelze znázornit tak jednoduše jako počet 7 – sedm víček, čárek, … a je třeba hledat vhodnější způsob, např. časová osa, tabulka, úsečka apod.
Dále jsou uvedeny ilustrace čtyř úloh (Ú1 – Ú4), které jsou z hlediska matematiky stejné, neboli mají stejný matematický model: 4 + 2 = 6.
První dvě úlohy jsou o věku, kde číslo je jako veličina (9). Ve druhých dvou úlohách číslo označuje počet. Na základě porovnání těchto dvou úloh o věku a dvou úloh o kuličkách je možné si uvědomit obtíže úloh o věku a rozdíl mezi dynamickou a statickou úlohou. (8)
U1. Alešovi jsou 4 roky a Bedřich je o 2 roky starší. Kolik let je Bedřichovi?
U2. Alešovi jsou 4 roky. Kolik mu bude za 2 roky?
U3. Aleš má 4 kuličky. Bedřich má o 2 kuličky více. Kolik kuliček má Bedřich?
U4. Aleš měl 4 kuličky. Ve hře 2 kuličky vyhrál. Kolik kuliček má Aleš po hře?
Úlohy U3 a U4 lze snadno znázornit a tím pádem žáci snadněji použijí strategii modelování (např. pomocí víček, kuliček na počítadle apod.), případně i grafickou vizualizaci, např.
U3. Aleš
![]()
Bedřich
![]()
U4. Aleš před hrou
![]()
Aleš po hře
![]()
Obr. 8 Grafická vizualizace slovní úlohy
Obě dvě úlohy lze jednoduše vizualizovat pomocí např. teček, což je stále dostupné vizuálnímu (případně i haptickému) vjemu žáka.
Problémem úloh U1 a U2 je, jak uchopit věk, jak znázornit graficky nebo modelem např. 7 let. Děj úlohy U1 se odehrává v jednom čase, nyní. Je to tedy úloha statická. Děj úlohy U2 se odehrává ve dvou různých časech (nyní a potom, za 2 roky), a proto jde o úlohu dynamickou. Slovní úlohy o věku mohou být tedy jak statické, tak dynamické. (8)
Obtížnost znázornit situaci slovní úlohy o věku, které by mohlo být východiskem pro řešení úlohy, se ukázalo jako velmi obtížné i pro žáky, kteří jsou běžně zvyklí vizualizaci k řešení používat.
Komentář učitelky 2. ročníku ZŠ
S vizualizací nebo manipulací pracuji s žáky běžně a žáci jsou i zvyklí obojí využívat, každý podle osobní preference a také podle situace zadané úlohy. Když jsem však žákům zadala slovní úlohu o věku, i žáci, kteří byli schopni tuto úlohu vyřešit, nevěděli, jak svůj způsob řešení zapsat. V žákovských řešeních se tedy nejčastěji objevilo pouze číslo 9, nebo párkrát matematický zápis situace (viz následující obr.).

Obr. 9. Řešení 9
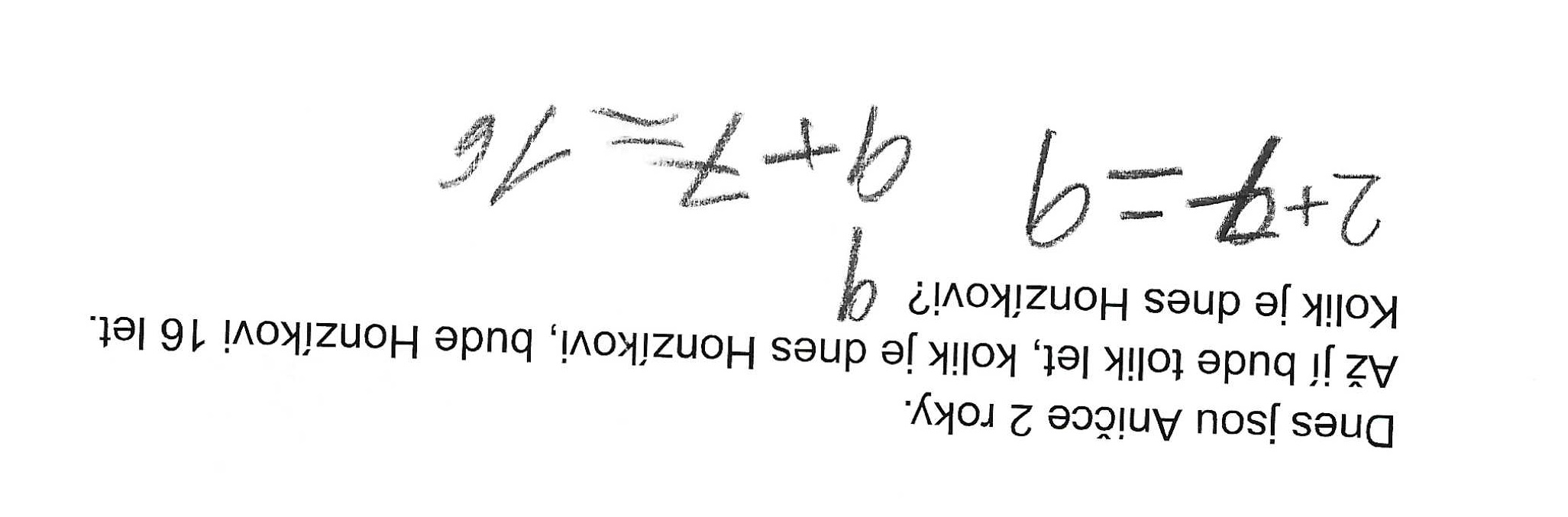
Obr. 10. Řešení 9 a ověření
Žáci, kteří nedokázali řešit úlohu pouze v mysli nebo pomocí čísel, nebyli schopni si situaci zobrazit, a tedy ji vůbec uchopit.
Hledáním možností, jak řešení úlohy zobrazit, modelovat nebo zapsat jsme se tedy věnovali v rámci společné diskuze, kdy žáci sdíleli a postupně rozvíjeli své nápady. Objevila se např. metoda pokus-omyl, kdy žáci zkoušeli volit různá čísla, kolik by mohlo být Honzíkovi let a své tipy ověřovali podle zadání. Zkoušeli také udělat nějaký zápis úlohy, který však sami uznali, že je pro tuto úlohu nesmyslný, protože jej vnímali jen jako přepis informací z textu do jednotlivých řádků. Ten, kdo doposud obsahu zadání slovní úlohy neporozuměl, tomu tento způsob stejně nepomohl. Až v závěru diskuze přišla jedna dívka s nápadem využít číselnou osu. Sama sice tuto myšlenku ještě neuměla zcela využít, ale tento způsob ostatní žáky natolik zaujal, že jej dále rozvíjeli až jím byli schopni situaci úlohy modelovat.
Videozkázka: Fragment z hledání žáků, jak by bylo možné úlohu modelovat pomocí krokovacího pásu
https://drive.google.com/file/d/1TUAzpYwOkoSMyjSeeJ0809VWjVu42cbg/view?usp=sharing
Když jsem asi o týden později dala žákům znovu obdobnou úlohu o věku, v mnohých řešení žáků se již objevilo využití číselné osy. A to dokonce i u žáků, kteří napoprvé nebyli schopni s úlohou hnout. Nyní díky nově objevené strategii byli již také úspěšnými řešiteli.

Obr. 11. Řešení na číselné ose
Co je klíčové pro celý řešitelský proces?
Je to vrstva příběhu či situace. Žák, který si nedovede představit situaci úlohy, nemůže ji vyřešit s porozuměním, nebo má velké obtíže, jak bylo výše ilustrováno. Tedy chceme dát žákům takové zkušenosti, na základě nichž si budou moci vytvořit o situaci představy (neboli si vytvořit situační model). Příležitost pro vytvoření vhledu do úlohy a dobrých představ nabízí dramatizace, jakožto příležitost prožít situaci vlastním tělem. Takové prožitky jsou základem pro kvalitní porozumění a tvorbu představ.
3. Proč jsou slovní úlohy o věku náročné?
Výchozí pro další zamýšlení bude následující úloha, která je zachycena i na videoukázce práce třídy.
U5.
Dnes jsou Toníkovi tři roky.
Až mu bude tolik let, kolik je dnes Aničce, bude Aničce 15 let.
Kolik je dnes Aničce?
Co způsobuje náročnost úlohy?
Náročnost úlohy způsobuje několik jevů.
Práce s časem
Příběh se odehrává ve dvou různých časech – dnes a potom. Dnes jsou Toníkovi 3. Věk Aničky dnes však neznáme. Potom – Aničce je 15 let, Toníkovi je tolik, kolik je dnes Aničce.
Komplikace spočívá v tom, že tok času se těžko modeluje a znázorňuje. Každý obrázek je statický jev (koncept), ale zde je děj, průběh času (proces).
Splnění dvou podmínek
Je potřeba splnit současně dvě podmínky, které se odehrávají v různých časech: dnes jsou Toníkovi 3 roky a potom bude Aničce 15 let. Žáci při řešení úlohy, zejména při řešení dramatizací, nebo simulovanou dramatizací poznávají, nebo si zvědomují dva důležité časové jevy: 1) Všichni stárnou stejně rychle, 2) věkový rozdíl dvou osob je stále stejný.
Složená úloha s nevyslovenou otázkou
Klíčem k řešení úlohy je zjistit dobu, která uplynula mezi dvěma časy “dnes” a “potom”. Na tento údaj však není zaměřena pozornost otázkou v úloze.
V zadání úlohy jsou čísla 15 a 2 v roli identifikátoru času (věku), tzn. adresy. Číslo 6, které hledáme, které je neznámé a vyjadřuje dobu uplynulou mezi dnes a potom, je operátorem změny. Řešením je číslo 9 – věk Aničky dnes, nebo věk Toníka potom, což je opět adresa.
Nelze použít postup naučený u typových úloh
Z tohoto pohledu je úloha netradiční.
Rovnost dvou údajů/věků, ale každý je v jiném čase, jeden je v budoucnu (Toník potom) a jeden je dnes (Anička dnes) (“až jí bude tolik, kolik je dnes …”).
Přítomnost antisignálu (10) Je znám věk Aničky potom, po uplynutí jisté doby, což signalizuje operaci sčítání. Avšak my se ptáme, kolik jí je dnes, tedy se v čase vracíme, čemuž odpovídá operace odčítání.
Slovo dnes
Žáci mohou mít zkušenost, že dnes je mi 9 let a mojí sestře 11. Ale zítra mi bude 10 a mojí sestře stále 11. Tento jev se v úloze nepředpokládá. Situace v úloze je proti reálné situaci zjednodušena. Může se říci, že Toník a Anička dnes slaví své narozeniny.
4. Dramatizace úlohy – hra Chronos
Nástroj na uchopení úlohy pomocí dramatizace je například tzv. Hra na boha Chrona. (Zpracováno podle námětů M. Hejného.) Chronos je bůh času a žák, který ho hraje, postupné oznamuje, jak plyne čas. Říká: “Jeden rok uplynul, teď.” Další dva žáci, kteří představují postavy v úloze (u nás tedy Anička a Toník) se pohybují po číselné ose připravené na podlaze např. pomocí lístečků s čísly. Další žák má roli hlasatele a vždy ohlašuje, jaká je situace po uplynutí každého dalšího roku. Podle jeho hlášení pak zapisovatel zanáší údaje do připravené tabulky. Klíčovou roli ve hře má také režisér, který hru zahajuje a pak rozhoduje, kdy hra skončí. Tuto roli nejprve zastává učitel, později ji přebírá žák nebo, jak je možné vidět na videoukázce, tuto roli může převzít zbytek třídy.
Ilustrace: https://www.youtube.com/watch?v=c1gJwjNAPH4
Ukázka zachycuje žáky 2. ročníku. Ti se před řešením úlohy seznámili s pravidly hry a vyzkoušeli si role. Poté již byli schopni hru použít pro vyřešení úlohy.
—————————————————————————————————————-
(11)
Přepis videa
- Žák přečte úlohu.
- Dnes jsou Toníkovi tři roky.
- Až mu bude tolik let, kolik je dnes Aničce, bude Aničce 15 let.
- Kolik je dnes Aničce?
- Role: Anička, Toník, zapisovatel, hlasatel, Chronos.
- Učitel/režisér navrhuje žákům, aby zkusili, kolik je Aničce let.
- Žáci navrhují 6 let.
- Režisér: Anička se postaví na 6 a tuto značku si označí. Toník stojí na 3.
- Zapisovatel: Zapíše výchozí situaci do tabulky.
Toník | 3 | |||||||||||
Anička | 6 |
- Režisér: Kam se má Anička dostat?
Na číselné ose je značka na čísle 15. - Chronos: Uplynul rok, teď. (Tleskne a spolu s ním všichni přihlížející žáci).
- A a T oba udělají jeden krok dopředu
- Hlasatel: Aničce je teďka 7 a Toníkovi 4.
- Zapisovatel zapisuje údaje 7, 4 do tabulky.
- Chronos: Uplynul rok, teď. (Tleskne a spolu s ním všichni přihlížející žáci).
- A a T oba udělají jeden krok dopředu.
- Hlasatel: Aničce je teďka 8 a Toníkovi 5.
- Zapisovatel zapisuje údaje 8, 5 do tabulky.
- Chronos: Uplynul rok, teď. (Tleskne a spolu s ním všichni přihlížející žáci).
- A a T oba udělají jeden krok dopředu.
- Hlasatel: Aničce je teďka 9 a Toníkovi 6.
- Zapisovatel zapisuje údaje 9, 6 do tabulky.
Toník | 3 | 4 | 5 | 6 | ||||||||
Anička | 6 | 7 | 8 | 9 |
- [Režisér hlásí, že hra končí, protože Toníkovi je 6. Ale Aničce není 15, proto se pokus nezdařil.]
- Jakmile Chronos odpočítal další rok, někteří žáci si všimli, že Toníkovi je už 6, tedy tolik, kolik bylo na začátku hry Aničce. Pokus končí nezdarem. Žáci navrhují věk Aničky pro další pokus – 7, 8, 9.
- Režisér: Anička se postaví na 9 a tuto značku si označí. Toník stojí na 3.
- Hlasatel: Toníkovi je teďka 3 a Aničce 9.
- Zapisovatel: zapíše výchozí situaci do tabulky.
Toník | 3 | |||||||||||
Anička | 9 |
- Na číselné ose je stále značka na čísle 15.
- Učitel: Proč odhadujete 9, jak jste na to přišli? Dvě děti vysvětlují a ukazují, že již mají do úlohy vhled.
- Chronos: Uplynul rok, teď. (Tleskne a spolu s ním všichni přihlížející žáci).
- A a T oba udělají jeden krok dopředu
- Hlasatel: Aničce je teďka 10 a Toníkovi 4.
- Zapisovatel zapisuje údaje 10, 4 do tabulky.
- Chronos: Uplynul rok, teď. (Tleskne a spolu s ním všichni přihlížející žáci).
- A a T oba udělají jeden krok dopředu.
- Hlasatel: Aničce je teďka 11 a Toníkovi 5.
- Zapisovatel zapisuje údaje 11, 5 do tabulky.
- Chronos: Uplynul rok, teď. (Tleskne a spolu s ním všichni přihlížející žáci).
- A a T oba udělají jeden krok dopředu.
- Hlasatel: Aničce je teďka 12 a Toníkovi 6.
- Zapisovatel zapisuje údaje 12, 6 do tabulky.
- Chronos: Uplynul rok, teď. (Tleskne a spolu s ním všichni přihlížející žáci).
- A a T oba udělají jeden krok dopředu.
- Hlasatel: Aničce je teďka 13 a Toníkovi 7.
- Zapisovatel zapisuje údaje 13, 7 do tabulky.
- Chronos: Uplynul rok, teď. (Tleskne a spolu s ním všichni přihlížející žáci).
- A a T oba udělají jeden krok dopředu.
- Hlasatel: Aničce je teďka 14 a Toníkovi 8.
- Zapisovatel zapisuje údaje 14, 8 do tabulky.
- Chronos: Uplynul rok, teď. (Tleskne a spolu s ním všichni přihlížející žáci).
- A a T oba udělají jeden krok dopředu.
- Hlasatel: Aničce je teďka 15 a Toníkovi 9.
- Zapisovatel zapisuje údaje 15, 9 do tabulky.
Toník | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||
Anička | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
- Žáci si zatleskají, vyšlo to.
- Režisér: Naše hra končí, protože Aničce je 15 a Toníkovi 9.
Co žáci poznali? S čím získali zkušenost?
Sehrávka umožnila žákům v krátkém čase uvidět, že
- Čas, který uplyne od DNES do POTOM, je stejný pro Aničku i Toníka. Jinak řečeno, všichni stárneme stejně rychle.
- Věkový rozdíl dvou lidí se časem nemění.
To jsou klíčové zákony o plynutí času a podstatné zkušenosti pro řešení dynamických úloh o čase, které je potřeba znát, abychom uměli zapsat vztahy mezi danými a hledanými údaji matematickým zápisem. Žáci navíc poznali, jak evidovat proces. Vhodným nástrojem je například tabulka. Ta zde hraje důležitou roli do budoucna. Žáci budou postupně opouštět sehrávku a ponechají si pouze tabulku, která je ale podepřena představou o ději. Tabulka se tak stane dalším nástrojem řešení takovýchto úloh. Později, ve 4.-5. ročníku, ji budou žáci ještě zjednodušovat výběrem klíčových údajů. Poslední tabulka tak dostane tuto podobu:
DNES | POTOM | |
Toník | 3 | 9 |
Anička | 9 | 15 |
Číslo 9 je hledaný údaj, který žáci při přepisu zadání do zkrácené tabulky napíší např. A-dnes.
Máme však zkušenosti s tím, že i dospělí raději pracovali s celou tabulkou, ve které totiž dobře viděli plynutí času. Úlohy pak ale řešili strategií pokus–ověření–korekce. Takováto zkrácená tabulka již snadno přivede žáky k matematickému přepisu vztahů mezi zadanými a hledanými údaji, neboli k rovnici např. A – 3 = 15 – A. Rovnice je obvykle nástroj pro uchopení úloh tohoto typu pro žáky na vyšším stupni.
DNES | POTOM | |
Toník | 3 | A-dnes |
Anička | A-dnes | 15 |
Dramatizací hrou na boha Chrona spolu s evidencí průběhu času do tabulky jsou tak i žáci 2. ročníku schopni sami vyřešit celkem náročnou úlohu.
5. Soubor slovních úloh o věku pro 2. a vyšší ročníky
(Částečně převzato z výukových materiálů prof. Milana Hejného pro studenty učitelství pro 1. stupeň ZŠ na PedF UK.)
Posledních pět úloh je vhodných pro starší žáky.
U1. Za dva roky mi bude 7 let. Kolik mi je let nyní?
U2. Mám bratra a ten je o 2 roky starší než já. Je mu 7 let. Hádej, kolik mi je let?
U3. Můj o dva roky starší bratr má dnes 11 let. Kolik je mi teď let?
U4. Za dva roky uplyne 8 let od chvíle, co jsem se narodil. Kolik mi je let?
U5. Můj o dva roky starší bratr se narodil před 10 lety. Kolik mi je let?
U6. Můj kamarád je přesně o rok starší než já. Dohromady nám je 11 let. Kolik let je mně a kolik mému kamarádovi?
U7. Eva je o 4 roky starší než Bětka. Dohromady jim je 22 let. Kolik je Evě?
U8. Sestrám Kláře a Lence je dohromady 19 let. Kláře byly 3 roky, když se Lenka narodila. Kolik let je dnes Kláře a kolik Lence?
U9. Dnes je Adamovi 5 let a Borisovi 9. Kolik bude Adamovi, až Borisovi bude 11 let?
U10. Dnes je Adamovi 5 let a Borisovi 9. Kolik bude Borisovi, až bude Adamovi 11 let?
U11. Je mi 8 let a mému bratrovi Oldovi je 14. Kolik let bude Oldovi, až já budu tak starý, jako je teď on?
U12. Dnes je mé mamince 34 let a mně je 8. Kolik bude mamince, až mně bude tolik, kolik jí je dnes?
U13. Dnes je mé mamince 34 let a mně je 8. Kolik mně bude let, až maminka bude mít dvakrát tolik let, co má dnes?
U14. Edovi je 19 let. Má o tři roky mladší sestru Elu. Jejich tatínkovi je 47 let. Kolik let bude Ele, až Eda bude tak starý, jako je nyní jejich tatínek?
U15. Dnes jsou Borisovi 3 roky. Až mu bude tolik, kolik je dnes Adamovi, bude Adamovi 11 let. Kolik let je dnes Adamovi?
U16. Alešovi jsou 3 roky. Až mu bude tolik, kolik je Borkovi dnes, bude Borkovi tolik, kolik je dnes Cyrilovi a Cyrilovi bude 39 let. Kolik je dnes Borkovi? Kolik let je dnes dohromady Alešovi, Borkovi a Cyrilovi? Kolik jim bude dohromady, až bude Cyrilovi 39 let?
U17. Dnes je Adamovi 9 let. Až mu bude tolik, kolik je Borisovi dnes, bude oběma dohromady 51 let. Kolik je dnes Borisovi?
U18. Adam a Boris jsou předškoláci. Až bude mít Adam tolik let, kolik má Boris dnes, bude mít Boris tolik, co měli Adam a Boris dohromady v době, když Adamovi byly 3 roky. V té době byl Boris o 1 rok mladší, než je Adam dnes. Kolik let je dnes Adamovi a kolik Borisovi?
U19. Mám 15letého bratra. Náš věkový průměr je 13 let. Kolik mi je?
U20. Jsem z dvojčat. Máme ještě jednu šestnáctiletou sestru. Věkový průměr nás tří je 12 let. Kolik mi je?
6. Výsledky slovních úloh
U1. Je mi 5 let.
U2. Je mi 5 let.
U3. Je mi 9 let.
U4. Je mi 6 let.
U5. Je mi 8 let.
U6. Mně je 5 let a kamarádovi 6 let.
U7. Evě je 13 let a Bětce 9 let.
U8. Lence je 8 let a Kláře 11 let.
U9. Adamovi bude 7 let.
U10. Borisovi bude 15 let.
U11. Oldovi bude 20 let.
U12. Dnes je mé mamince 34 let a mně je 8. Kolik bude mamince, až mně bude tolik, kolik jí je dnes?
U12. Mamince bude 60 let.
U13. Bude mi 42 let.
U14. Ele bude 44 let.
U15. Adamovi je dnes 7 let.
U16. Borkovi je dnes 15 let. Dohromady jim je dnes 45 let. Až bude Cyrilovi 39 let, bude jim dohromady 81 let.
U17. Borisovi je dnes 20 let.
U18. Adamovi je 5, Borisovi 6 let.
U19. Bratrovi je 11 let.
U20. Je mi 10 let.
———————————————————————————————————————–
(1) Slovními úlohami rozumíme úlohy s (pseudo-)reálným kontextem. Některé číselné údaje jsou dány, některé se hledají na základě vztahů mezi nimi. Úkolem je matematizovat reálnou situaci. To znamená odhalit vazbu mezi údaji danými v zadání úlohy a určit, jaká číselná operace tyto vztahy mezi číselnými údaji popisuje. Výsledek úlohy je třeba ověřit jednak numericky, jednak sémanticky. Více ve (Vondrová, 2019, s. 61-62).
————————————————————————————————————–
(2) RENDL, M., VONDROVÁ, N. a kol. Kritická místa matematiky na základní škole očima učitelů. Praha: UK v Praze, PedF, 2013.
Obšírněji o slovních úlohách pojednává dále i monografie:
VONDROVÁ, N. a kol. Matematická slovní úloha: mezi matematikou, jazykem a psychologii. Praha: Karolinum, 2019
VONDROVÁ, N. Didaktika matematiky jako nástroj zvládání kritických míst v matematice. Praha: Pedagogická fakulta, Univerzita Karlova, 2019
—————————————————————————————————————-
(3) Jednou z možných cest, jak můžeme jako učitelé žákům pomoci zlepšovat se v porozumění slovním úlohám a ve schopnostech je řešit, je nabízet jim širokou paletu různých řešitelských strategií (3), tedy způsobů, jak je možné slovní úlohy uchopit a řešit.
—————————————————————————————————————-
(4) Tvorba situačního modelu – např. víčka místo koleček auta. Rozlišujeme různé úrovně podle míry abstrakce zástupného modelu. Tato strategie je vhodná zejména pro řešení statických úloh.
—————————————————————————————————————-
(5)Využívání grafické vizualizace probíhá na různých úrovních od úrovně sémantické, kdy žáci graficky znázorňují reálné objekty z úlohy, přes využití zástupného objektu, např. trojice koleček místo tříkolky, až po úroveň strukturálního uchopení (tabulka, schéma, graf, …), kde figurují pouze čísla. Vytvořením grafického vizuálního situačního modelu se stává z dynamické úlohy úloha statická. Proto jsou různé grafické vizualizace pro rozvoj schopnosti řešit slovní úlohy velice důležité.
Speciálním způsobem vizualizace statických úloh pomocí tzv. “bar modelů” se zabývá příspěvek Pavla Bobka (vložit proklik na příspěvek Pavla Bobka)
—————————————————————————————————————-
(6)Žák je účastníkem řešení úlohy a vlastním tělem prožívá situaci úlohy a její řešení. Tato strategie je vhodná zejména pro řešení úloh dynamických, tj. takových, kde příběh úlohy se odehrává v čase.
V rámci dramatizace můžeme mluvit i o tzv. simulované dramatizaci, kdy žák vytvoří situační model pomocí zástupných objektů, např. figurky, víčka apod. a děj simuluje sehrávkou např. s víčky. Je sice přímým účastníkem řešení úlohy, ale prostřednictvím nějakého zástupného objektu. Tato strategie je také vhodná zejména pro řešení úloh dynamických.
—————————————————————————————————————-
(7) Strukturální strategie se opírá o čistě matematický model, který využívá čísla nějak zorganizovaná, symboliku a početní operace
————————————————————————————————————————
(8) Úlohu nazýváme dynamickou, když v ní čas hraje důležitou úlohu, když se příběh úlohy odehrává ve dvou či více časových rovinách (např. dříve, nyní, za nějakou konkrétní dobu, potom).
V úlohách statických se vše odehrává teď nebo v jedné časové rovině.
Dynamické slovní úlohy jsou náročnější než úlohy statické. Jednou z příčin náročnosti je uchopení dynamického jevu – plynutí času a stárnutí osob. Druhou příčinou je zákonitost plynutí času, která je v úlohách skryta – všem osobám plyne čas stejně rychle.
—————————————————————————————————————-
(9) Ve slovních úlohách, při úvahách o jejich pestrosti, je vhodné sledovat to, co číslo v zadání úlohy znamená. Budeme uvažovat pouze o čísle jako kvantitě a vynecháme číslo jako identifikátor, např. dům číslo 48, i jako symbol, např. 13 je šťastné číslo. Číslo jako kvantita může označovat počet, např. 5 dětí, nebo veličinu, např. 5 metrů, litrů, kilogramů, …. Někdy nelze rozhodnout, zda se jedná o počet nebo veličinu. Například když řekneme 5 korun, není jasné, zda se jedná o 5 kusů jednokorunových mincí (počet), nebo o jeden kus mince 5 Kč (veličina). S číslem jako počtem má žák mnohem více životních zkušeností a takové situace se dobře modelují prsty, či jakýmikoliv manipulativy. Číslo jako veličina kolem sebe tolik nevnímáme a mnohem hůře se modeluje. Například 2 litry vody v hrnci, jeden kus provazu délky 2 m (veličina) asi nikdo, kdo si teprve buduje představy o číslech, nebude modelovat dvěma prsty, nebo kaštany, víčky apod.
Pro vnímání vazby mezi čísly ve slovní úloze je důležité, jakou roli čísla v dané situaci mají. Porovnejme tři situace, kde všechna čísla znamenají počet (kaštanů):
- Mám v jedné ruce 2 kaštany a ve druhé 3 kaštany. Dohromady mám 5 kaštanů.
- Mám 2 kaštany a kamarád mi přidal 3 kaštany. Mám nyní 5 kaštanů.
- Mám 2 kaštany, Honza má o tři kaštany více. Honza má 5 kaštanů.
Číslo 2 má ve všech třech situacích stejnou roli. Říkáme jí stav. Číslo 3 má v situaci A také roli stavu, ale v situaci B vyjadřuje změnu – této roli říkáme operátor změny, a v situaci C číslo 3 porovnává jiné dva stavy, 2 a 5. Této roli říkáme operátor porovnání. Více viz (Vondrová, 2019, s. 63; Hejný, 2014, s. 153-158) (2)
—————————————————————————————————————-
(10) Slovní úlohy s antisignály
Slovní úlohy s antisignálem jsou specifické tím, že v zadání úlohy je přítomno signální slovo, které poukazuje na jistou operaci, např. dohromady, více, přibylo, … (operace sčítání), nebo méně, odešli, ubylo, … (operace odčítání), ale k výpočtu je potřeba použít operaci opačnou (inverzní).
Příklad slovní úlohy se signálem:
Milan s Vaškem sbírají modely aut. Milan má již ve své sbírce 18 modelů. Vašek jich má ale o 7 více. Kolik modelů aut má Vašek?
V zadání slovní úlohy je slovo více signální. Poukazuje na operaci sčítání a tuto početní operaci je potřeba provést při řešení.
Již malou obměnou zadání je možné stejnou úlohu naformulovat antisignálně:
Milan s Vaškem sbírají modely aut. Vašek má ve své sbírce 25 modelů. Má tak o 7 modelů více než Milan. Kolik modelů aut má Milan?
I zde je přítomno slovo více. Tentokrát však je třeba použít operaci odčítání. Slovo více je tedy v tomto zadání antisignál. Vašek má 25 aut a má jich více než Milan. Pro řešitele je tedy nutné si uvědomit, že Milan je ten, kdo jich má méně. Proto je nutné provést operaci odčítání, která je inverzní ke sčítání.
Ve školní praxi se žáci většinou setkávají s úlohami, při kterých je strategie signálních slov úspěšná. Úlohy obvykle uchopují tak, že vyhledávají slova a ta propojují na odpovídající početní operace. A tak práce pouze se strategií signálních slov vede žáky k formální, povrchové znalosti a při výskytu antisignálu chybují. Úlohy s antisignálem mohou také mimo jiné sloužit učiteli jako diagnostický nástroj pro identifikaci formální znalosti žáka a hlavně pro čtení s porozuměním. Učitel si tak může ověřit míru porozumění úlohové situaci i schopnost soustředěně pracovat s objekty a vztahy mezi nimi dané úlohou. Někteří učitelé sice mohou namítat, proč zadávat žákům úlohy, s jejichž řešením budou mít s největší pravděpodobností problémy. Důležité pro rozvoj poznávání žáků však je, aby se setkávali i s těmito náročnými situacemi. Významnou roli zde hraje práce učitele s chybou žáka. Velmi přínosné se v tomto případě ukazuje otevřít nad řešením žáka ve třídě diskuzi. Žáci porovnávají svá řešení, argumentují jejich správnost a formulují svým jazykem strategie řešení. Pokud se učitel vyzbrojí dostatečnou trpělivostí, dostanou žáci možnost získat hluboké vhledy do úloh, které při dostatečném množství vytvoří dobrý základ pro porozumění slovním úlohám a jejich řešitelským strategiím.
Práce žáků se slovními úlohami s antisignálem má 3 potence:
- žák si vytváří citlivost na antisignál a rozvíjí čtenářskou gramotnost,
- vytváří si také schopnost uchopit antisignální situaci,
- učí se korigovat její chybné uchopení na základě konfrontování s chybou v diskuzi se spolužáky
Více k problematice slovních úloh s antisignálem např. v:
Chaloupková, S.: Úlohy s antisignálem pro žáky 1. stupně ZŠ (diplomová práce). Pedf. UK, Praha 2009 (https://dspace.cuni.cz/handle/20.500.11956/21043)
ÚLOHY S ANTISIGNÁLEM VE 2. TŘÍDĚ
—————————————————————————————————————-
