SLOVNÍ ÚLOHY nejen řešíme

Autor: Filip Roubíček, ZŠ sv. Voršily v Praze

Didaktický přístup ke slovním úlohám

Slovní úlohy bývají hodnoceny žáky i učiteli jako obtížné téma školské matematiky. Ptáme-li se po důvodech, proč tomu tak je, zjišťujeme, že to souvisí s tím, jak jsou úlohy didakticky pojímány a prezentovány a zejména jak se ve výuce přistupuje k jejich řešení. Nízká obliba řešení slovních úloh mezi žáky bývá způsobena absencí možnosti řešit úlohy po svém. Je-li žákovi vnucován požadavek, že slovní úlohu určitého typu musí řešit předepsaným způsobem, zákonitě to omezuje jeho tvůrčí přístup a schopnost samostatně řešit slovní úlohy. Toto tvrzení nelze chápat tak, že učitel nemá seznamovat žáky s řešením typových úloh a formami jejich záznamu. Standardizované postupy mají své místo ve výuce matematiky a mají smysl pro rozvoj řešitelských dovedností, nelze však na nich lpět s poukazem, že to tak je v učebnici. Stává se, že žáci dovedou správně řešit naučené typové úlohy, ale selhávají při řešení slovních úloh, které jsou jinak zadány (např. úlohy s antisignálem nebo úlohy s více řešeními) nebo vyžadují jiný postup než ten, který znají z řešení typových úloh. Příčinou selhání bývá mechanické zapamatování postupu bez porozumění a neschopnost postup řešení logicky vyvodit.

Existují různé cesty, jak vést žáky k tomu, aby se stali aktivními řešiteli s vlastními nápady, lépe porozuměli situaci popsané ve slovní úloze a dovedli ji správně matematicky uchopit. V tomto příspěvku se seznámíme jednou z nich. Na pěti slovních úlohách určených žákům prvního stupně ukážeme, jak může učitel přistupovat k řešení slovní úlohy v heterogenní skupině žáků, aby aktivoval ideálně všechny žáky a dovedl je k porozumění, o co v úloze jde, a jak lze z pohledu matematiky vytěžit situaci popsanou ve slovní úloze, aby tato aktivita přispěla k rozšíření a upevnění matematických poznatků.

Využití slovních úloh ve výuce

Vyučovací hodina, jež je zacílena na rozvoj dovedností řešit slovní úlohy, může mít následující scénář.

Učitel nejprve vyzve žáky, aby si zadání slovní úlohy pozorně přečetli, začali úlohu svým způsobem řešit a své řešení zaznamenávali (pro tyto účely je vhodné vytisknout zadání úlohy na volný list papíru). Důležité je ponechat jim dostatečný prostor pro samostatnou práci (případně jim umožnit řešit úlohy ve dvojicích), přičemž úkolem učitele je zejména motivovat žáky k řešení, vybízet je, aby zkusili nějak začít. Zaznamená-li u některého žáka obtíže s pochopením zadání, individuálně napoví (představ si, jak to probíhalo; nakresli si, co se dělo; zamysli se na tím, co říká tato věta). Pozoruje-li učitel nesnáze u více žáků, iniciuje diskusi ve třídě, při níž zadání ujasní a prostřednictvím návodných otázek pomůže s jejím správným uchopením. Při diskusi maximálně vychází z žákovských nápadů, které vhodně komentuje, aby naznačil, kudy se vydat, ale přitom neprozradil celý postup řešení. Samostatná práce je důležitým východiskem pro další práci, a to i v případě, že se žákům nepodaří úlohu správně uchopit, protože bez důkladného seznámení se zadáním úlohy nejsou schopni se do jejího řešení aktivně zapojit. Po samostatné práci následuje řízená diskuse ve třídě, kdy žáci prezentují, jak zadání úlohy porozuměli a jaké postupy řešení navrhují, a vysvětlují, jak uvažovali. Je důležité umožnit prezentaci více žákům, aby měli možnost se seznámit s několika různými postupy, přičemž nevadí, že se odlišují pouze způsobem záznamu. Přestože se zdá, že všichni si vědí s úlohou rady a postupují správně, učitel zrekapituluje s žáky celý proces řešení, aby mohl následně úlohu didakticky rozvinout.

U některé slovní úlohy je výhodné setrvat déle, protože matematická situace, kterou žáci v úloze řešili, je didakticky podnětná. Čas, který jsme věnovali jejímu řešení, se vyplatí zúročit tím, že se podíváme na řešenou problematiku z dalších hledisek, uvažujeme jiné podmínky, hledáme zobecnění apod. Zkrátka práce se slovní úlohou neskončí jejím vyřešením, ale nalezení výsledku se stane podnětem pro prozkoumání situace popsané v zadané úloze a řešení dalších souvisejících úloh. Smyslem „vytěžení“ slovní úlohy je dát prostor pomalejším řešitelům, aby si stihli uvědomit podstatu úlohy a všechny souvislosti a měli více příležitostí se do procesu řešení aktivně zapojit, a na druhou stranu také zdatnějším řešitelům, aby měli možnost tvořit k dané situaci nové úlohy, a tak rozvinout své řešitelské dovednosti. Nejen pro slabší žáky může být práce se známou (dobře uchopenou) situací a uvažování v jednom kontextu usnadněním jejich učení a porozumění.

Náměty pro další práci se slovní úlohou

Obměna slovní úlohy úpravou vstupních údajů (podmínek)
Zobecnění slovní úlohy v daném kontextu
Tvoření otázek a úkolů k dané slovní úloze
Tvoření slovní úlohy podle vzoru
Tvoření slovní úlohy s daným výsledkem

Předpokladem pro další práci se slovní úlohou je její vyřešení, proto v následujícím popisu je vždy uvedeno, jak žáci úlohu řešili. Prezentace různých (i chybných) řešitelských postupů s doprovodným vysvětlením je pro žáky inspirativní a nápomocné. Žáci musí správně uchopit zadanou situaci a získat vhled do podstaty problému, aby se mohli věnovat obměně slovní úlohy, jejímu rozšíření či zobecnění. Zároveň je třeba podotknout, že rozbor řešení úlohy a její následné rozpracování vyžaduje více času a často zabere celou vyučovací hodinu.

Obměna slovní úlohy úpravou vstupních údajů

Žákům třetího ročníku byla zadána následující slovní úloha s časovými údaji:

(Obrázek č.1 – Úloha je převzata z Učebnice matematiky pro 3. ročník autorského kolektivu prof. Hejného, H-mat, 2020, str. 25.)

Zkrácený záznam dialogu učitele (U) s žáky (Ž):

U: Jak jste pochopili, o co v úloze jde?
Ž: Terka a Aneta jezdily na koloběžce a střídaly se.
U: Jak se střídaly?
Ž: Každá jezdila vždy čtvrt hodiny.
U: Jak jste si střídání koloběžky zaznamenali? Kdo by chtěl ukázat svůj zápis na tabuli?

Několik žáků prezentuje na tabuli záznam střídání v podobě seznamu časových úseků, k nimž jsou přiřazena jména.

Obrázek č. 2 – Ukázka žákovského řešení

U: Zapsal to někdo jinak?
Ž: Mám to stejně, ale psal jsem jen minuty a místo jmen písmena A, T.

Obrázek č. 3 – Ukázka žákovského řešení

Ž: Časy mám v řádce za sebou.

Obrázek č. 4 – Ukázka žákovského řešení

U: Použil někdo časovou osu?

Učitel ukazuje další možnost záznamu, který mohli žáci použít. Kreslí na tabuli časovou osu.

Obrázek č. 5 – Ukázka zápisu na tabuli

U: Které časové údaje je nutné vyznačit?
Ž: Musí tam být, kdy začali jezdit a kdy skončili.
Ž: A taky půlhodinová přestávka a kdy Aneta spadla.
U: Proč tam musí být čas pádu?
Ž: Abychom věděli, kdy jela Aneta a kdy Terka, jak se střídaly.
U: Které z děvčat tedy jelo první na koloběžce?
Ž: První jela Aneta, protože mi to tak vyšlo v tom seznamu.
U: Přišel na to někdo jiným způsobem?
Ž: Vypočítala jsem, že do přestávky jezdily dvě hodiny, tedy každá jela čtyřikrát. Po přestávce jezdily už jen hodinu a tři čtvrtě. Po přestávce jela první Aneta, protože spadla, a nakonec vlastně i skončila.

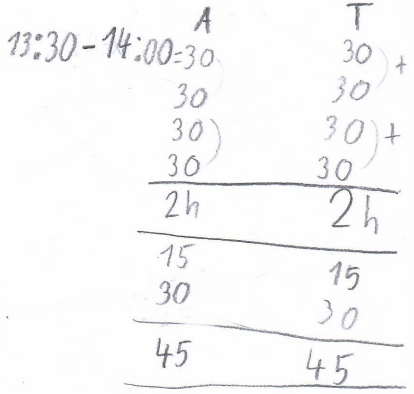
Obrázek č. 6 – Ukázka žákovského řešení

U: A ve 13:30 jela první taky Aneta?
Ž: Ano, protože jinak by se to nestřídalo.
U: Kolik minut celkem každá z nich jezdila?
Ž: Aneta jezdila 120 minut a Terka 105.
U: Co myslíte, bylo střídání koloběžky spravedlivé?
Ž: Nebylo.
U: Proč to nebylo spravedlivé?
Ž: Protože Aneta začala i skončila.
Ž: Protože Terka jezdila kratší čas.
U: Co by se muselo změnit, aby střídání koloběžky bylo spravedlivé?
Ž: Musely by začít jezdit o 15 minut dřív anebo později.
Ž: Nebo by musely skončit až v šest hodin.
Ž: Taky by mohla být kratší přestávka, jen 15 minut.
Ž: Nebo naopak delší.
U: Jak se řešení úlohy změní, když by se střídala tři děvčata (navíc Monika)? Zkusme upravit časovou osu, kterou už máme na tabuli. Co tam můžeme nechat?
Ž: Začátek a konec jízdy.
Ž: A přestávku půl hodiny.
Ž: Taky kdy Aneta spadla. Od Anety se to bude střídat.
U: Jak se budou střídat?
Ž: Aneta, Terka, Monika atd.
Ž: Nebo nejdřív Monika a pak Terka.
U: Takže máme dvě možnosti? Která z nich tedy jela první?
Ž: První jela Terka, nebo Monika.
U: Kolik minut každá z nich jezdila?
Ž: Každá jela pětkrát, tedy celkem 75 minut.
U: Bylo v tomto případě střídání koloběžky spravedlivé?
Ž: Všechny by jezdily stejně dlouho, ale musely by dlouho čekat?

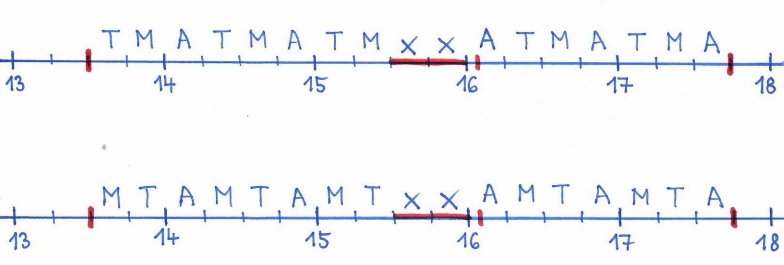
Obrázek č. 7 – Ukázka zápisu na tabuli

Z dialogu učitele s žáky je patrné, že proces řešení úlohy neskončil nalezením odpovědí na zadané otázky. Učitel využil nastalé didaktické situace: vybídl žáky, aby se zamysleli nad změnou vstupních parametrů zadané úlohy (Co by se muselo změnit, aby střídání koloběžky bylo spravedlivé?), a následně jim zadal úlohu s jiným počtem děvčat (Jak se řešení úlohy změní, když by se střídala tři děvčata?). V ukázce není zmíněna další možnost, a to změna délky časového úseku pro střídání koloběžky (např. střídání koloběžky po deseti minutách). Úprava zadání slovní úlohy změnou některých vstupních údajů vede žáky k přemýšlení nad podstatou problému a umožňuje jim lépe pochopit význam jednotlivých údajů a jejich vzájemné souvislosti.

Zobecnění slovní úlohy v daném kontextu

Žáci 5. ročníku samostatně řešili slovní úlohu na dělitelnost:

(Obrázek č. 8 – Úloha je převzata z učebnice Pěchoučková, Š.: Matematika se čtyřlístkem 5, FRAUS, 2015, str. 21.)

Své postupy řešení prezentovali na tabuli. Většina žáků použila stejný postup, odlišnosti byly pouze ve formě zápisu. Nejprve určili počet žáků ve čtyřech stejně početných skupinách (výpočet 29 – 5 = 24) a pak určili počet žáků v jedné skupině (výpočet 24 : 4 = 6). Někteří zapsali oba kroky do jednoho výpočtu.

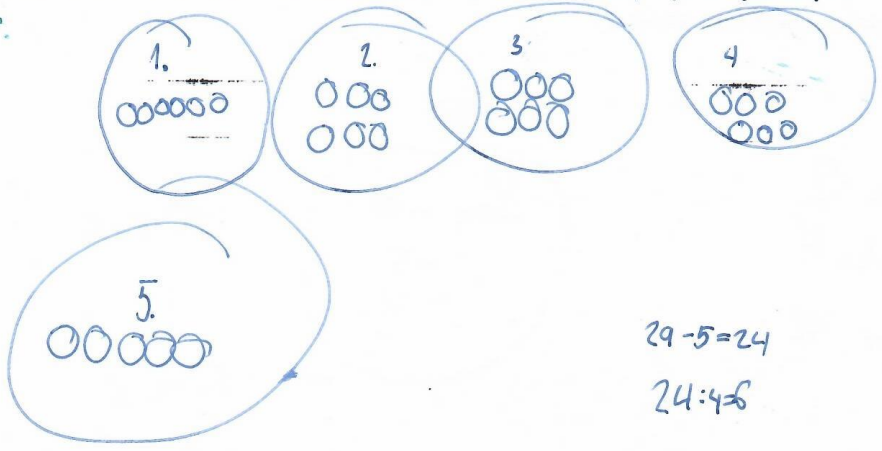
Obrázek č. 9 – Ukázka žákovského řešení

Obrázek č. 10 – Ukázka žákovského řešení

Poté učitel zadal navazující úkol:

U: Jaký jiný počet žáků ve třídě by bylo možné zadat, když ostatní podmínky v úloze zůstanou stejné?

Žáci sami počítají a hledají jiné počty, se kterými úloha vychází.

U: Na co jste přišli?
Ž: Myslím, že jich bude dvacet pět, o čtyři míň. Ve všech skupinách je pět žáků.
U: Má někdo jiný počet?
Ž: Já mám dvacet jedna. 21 – 5 = 16 a 16 : 4 = 4.
U: Našel někdo počet větší než dvacet devět?
Ž: Mně vyšlo čtyřicet jedna.
U: Jak jsi na to přišel?
Ž: Použil jsem svůj výpočet 6 . 4 = 24 a 24 + 5 = 29. Místo šesti jsem napsal devět a vyšlo mi, že 9 . 4 = 36 a 36 + 5 = 41.

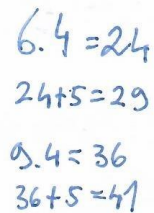
Obrázek č. 11 – Ukázka žákovského řešení

U: Proč právě devět?
Ž: To jsem si tipnul.
Ž: Já jsem počítal se sedmičkou a vyšlo mi třicet tři.
U: Použil někdo jiný postup?
Ž: Já jsem k číslu dvacet devět přičítal čtyři a dostal jsem 33, 37, 41, 45 atd.

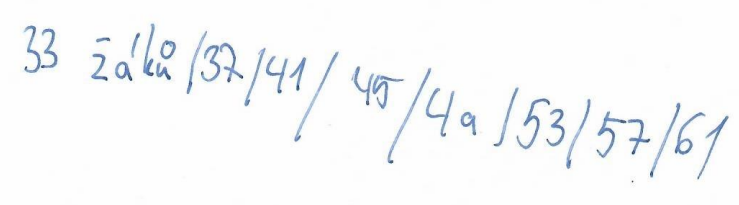
Obrázek č. 12 – Ukázka žákovského řešení

U: Vidíte v řadě čísel 21, 25, 29, 33, 37, 41, 45… nějakou pravidelnost?
Ž: Ta čísla se zvětšují o čtyři.
U: Proč zrovna o čtyři?
Ž: Aby v těch čtyřech skupinách byl stejný počet dětí.
U: Jak bychom mohli všechny tyto počty zapsat?
Ž: Mně napadla rovnice x . 4 + 5 = y.
U: Co je v této rovnici x a y?
Ž: Písmenem x jsem označila, kolik dětí je ve skupině, a y, kolik jich je dohromady.
U: Našli jsme několik možností a dokonce obecný předpis. Co myslíte, jaké počty můžeme použít do zadání slovní úlohy, aby byla smysluplná? Mohlo by být v páté třídě 41 žáků?

Zadaná slovní úloha nebyla pro žáky nijak obtížná, proto se učitel rozhodl s úlohou dále pracovat a uvažovat jiné počty žáků ve třídě. Žáci na jeho pokyn spontánně zareagovali a vymysleli několik možností včetně zobecnění. V závěru diskuse je učitel upozornil, aby zvažovali jen ty možnosti, které odpovídají reálnému kontextu zadané úlohy (možnému počtu žáků v běžné třídě).

Tvoření otázek a úkolů k dané slovní úloze

Žáci 5. ročníku řešili slovní úlohu, která je zaměřena na dělení celku na části a porovnání rozdílem a podílem:

Obrázek č. 13 – Screen textu k úloze z testu JPZ (Cermat)

Žáci prezentovali na tabuli, jak úlohu řešili. Někteří žáci vypočítali jednotlivé vzdálenosti ze zadaných vztahů na základě logické úvahy, příp. využili také nákres, jak je celek rozdělen na části.

Obrázek č. 14 – Ukázka žákovského řešení

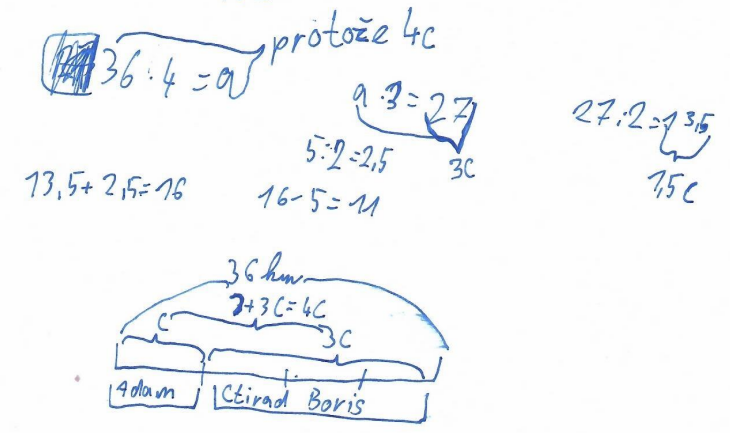
Obrázek č. 15 – Ukázka žákovského řešení

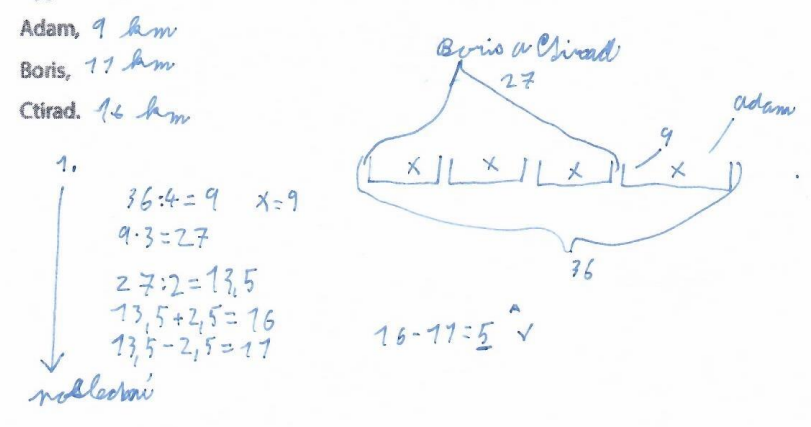
Obrázek č. 16 – Ukázka žákovského řešení

Jiní využili metodu pokus a omyl, zkoušeli různé kombinace čísel, aby byly splněny zadané podmínky, případně vypsali všechny možnosti a z nich vybrali tu správnou.

Obrázek č. 17 – Ukázka žákovského řešení

Obrázek č. 18 – Ukázka žákovského řešení

Po vysvětlení různých žákovských postupů následovala diskuse k řešení úlohy, při které učitel vyzval žáky, aby zadaní úlohy pozměnili a upravenou úlohu vyřešili.

Žáci k původnímu zadání vymysleli jinou otázku nebo úkol.

O kolik více kilometrů uběhl Ctirad než Adam?

16 – 9 = 7

Kdo z nich běžel nejpomaleji, když každý z nich běžel stejně dlouho?

Jak velkou část závodu uběhl Ctirad?

16/36 = 4/9

Žáci vytvořili novou úlohu z původního zadání buď změnou zadaných údajů, nebo jejich doplněním.

Boris se Ctiradem uběhli dohromady třikrát delší vzdálenost než Adam. Ctirad uběhl o 5 km delší vzdálenost než Boris. Kolik kilometrů každý z nich uběhl, jestliže uběhli dohromady 32 km?

32 : 4 = 8 (A)

32 – 8 = 24

24 – 5 = 19

19 : 2 = 9,5 (B)

9,5 + 5 = 14,5 (C)

Adam, Boris a Ctirad uběhli 36 km. Boris se Ctiradem uběhli dohromady třikrát delší vzdálenost než Adam. Adam uběhl o 5 km kratší vzdálenost než Boris. Kolik kilometrů uběhl Ctirad?

36 : 4 = 9 (A)

9 + 5 = 14 (B)

36 – 9 = 27

27 – 14 = 13 (C)

Adam, Boris a Ctirad uběhli 36 km za 3 hodiny. Boris se Ctiradem uběhli dohromady třikrát delší vzdálenost než Adam. Ctirad běžel o 15 minut déle než Boris. Jak dlouho každý z nich běžel? (Všichni běželi stejně rychle.)

3 h = 180 min

180 : 4 = 45 min (A)

180 – 45 = 135

135 – 15 = 120

120 : 2 = 60 (B)

60 + 15 = 75 (C)

4) Tvoření slovní úlohy podle vzoru

Žáci 3. ročníku řešili následující slovní úlohu s mincemi a bankovkami:

(Obrázek č. 19 – Úloha je převzata z Učebnice matematiky pro 4. ročník autorského kolektivu prof. Hejného, H-mat, 2021, str. 36.)

Úkoly a) a b) zvládli bez problémů. Diskuse vznikla k řešení části c). Žáci správně určili, že částku 210 Kč je třeba rozdělit na tři stejné části, ale došli k závěru, že to nejde, protože neexistuje mince s hodnotou 70 Kč. Z ukázek žákovských řešení je zřejmé, jak modelovali jednotlivé situace a jak určovali neznámé mince.

Obrázek č. 20 – Ukázka žákovského řešení

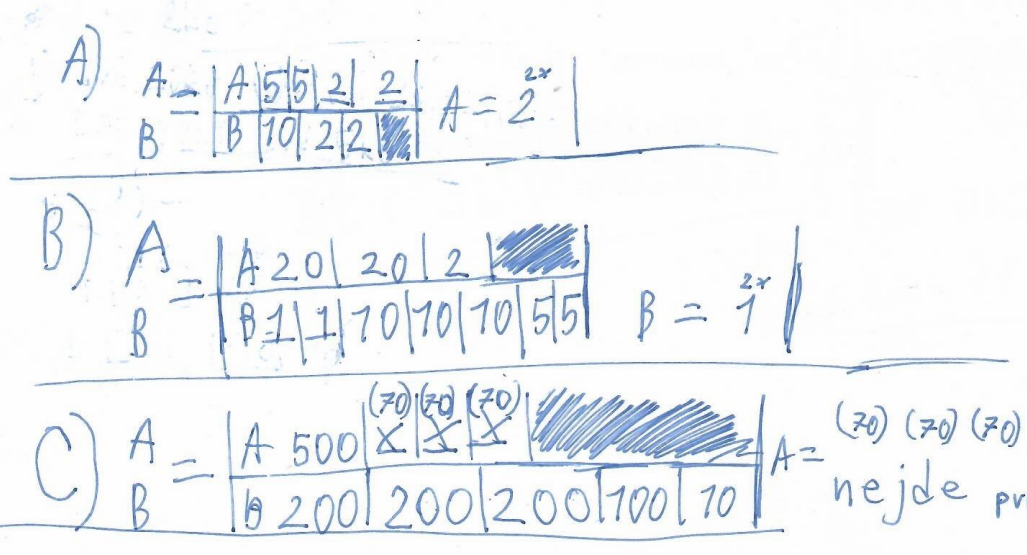
Obrázek č. 21 – Ukázka žákovského řešení

Poté byli žáci vyzváni, aby tvořili vlastní úlohu s obdobným zadáním. Inspirovali se předcházejícím řešením a vytvářeli různé kombinace mincí a bankovek.

Obrázek č. 22 – Ukázka žákovského řešení

Obrázek č. 23 – Ukázka žákovského řešení

Tvoření slovní úlohy s daným výsledkem

Žáci 5. ročníku řešili následující slovní úlohu se zlomky:

Z bonboniéry se 30 bonbony snědla Eliška 2/5 bonbonů. Terezka snědla o 2/3 méně než Eliška. Ondra vymlsal 3/4 toho, co Eliška s Terezkou dohromady. Kolik, kdo snědl bonbonů? Zbyly ještě nějaké pro Matěje?

(Úloha je převzata z učebnice Kozlová, M., Pěchoučková, Š., Rakoušová A.: Matematika se čtyřlístkem 4, FRAUS, 2014, str. 72.)

Žáci neměli žádné obtíže s určením části celku vyjádřené zlomkem, bylo však nutné dovysvětlit, co znamená formulace „o 2/3 méně než“, resp. z jakého celku se tato část počítá (dotaz žáka: „Dvě třetiny z čeho?“). Pro záznam řešení použili žáci většinou zápis do řádků, případně zjištěné počty zapsali do jednoduché tabulky. Části určovali pomocí jednoduchých výpočtů: celek vydělili jmenovatelem zlomku a výsledný podíl vynásobili čitatelem zlomku. Žádný z žáků nepoužil ve svém řešení obrázek (např. obdélník s 5×6 políčky), z čehož lze usuzovat, že buď nejsou zvyklí grafický model používat, nebo jej v této úloze nepotřebovali.

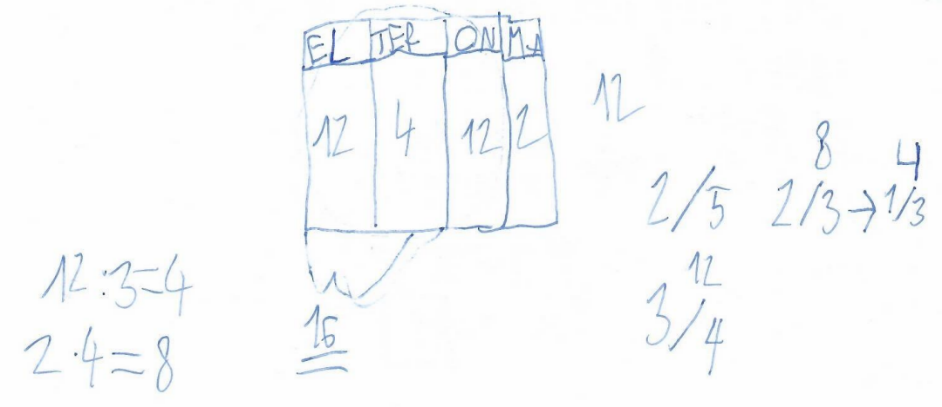
Obrázek č. 24 – Ukázka žákovského řešení

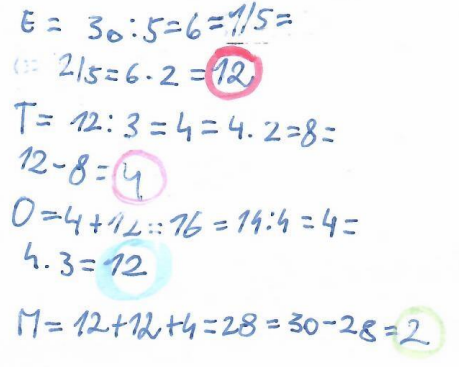
Obrázek č. 25 – Ukázka žákovského řešení

Po prezentaci žákovských řešení následovala diskuse (U-učitel, Ž-žáci):

U: Jaký údaj je třeba změnit v zadání úlohy, aby na Matěje zbylo více bonbonů?
Ž: Vzít bonboniéru, ve které bude víc bonbonů.
U: Kolik by muselo být v bonboniéře bonbonů?
Ž: Třeba šedesát.
U: Kolik bonbonů by pak na Matěje zbylo?
Ž: Dvakrát víc, tedy čtyři.
U: Jaký jiný údaj v zadání můžeme změnit, aby Matěj dostal více bonbonů? Počet 30 zůstane stejný.
Ž: Mohli bychom měnit ty zlomky.
U: Jak bys je měnil?
Ž: Eliška by snědla místo dvou pětin jen jednu pětinu.
U: Jak by se v tomto případě změnilo řešení úlohy?
Ž: Eliška by měla 6, Terezka jen 2, Ondra 6 a pro Matěje by zbylo 16.
U: Ondra by tentokrát dostal nejvíc. Stále nám ale vycházejí velké rozdíly mezi počty bonbonů, které dostaly jednotlivé děti. Co musíme změnit v zadání, aby se rozdíly zmenšily?
Ž: Kdyby každý dostal čtvrtinu, měli by stejně.
Ž: Ale to nejde. Třicet bonbonů nerozdělíš na čtvrtiny.
U: Museli bychom půlit bonbony a to nechceme. Jak jinak to udělat?
Ž: Já bych zmenšila všechny zlomky. Elišce pětinu, Terezce o třetinu méně, Ondrovi dvě čtvrtiny, vlastně polovinu…
Ž: To ti taky nevyjde.
U: Kolik by vyšlo na jednotlivé děti?
Ž: Eliška by měla šest bonbonů, Terezka čtyři a Ondra pět. To je docela vyrovnané.
Ž: Jenže Matějovi by zbylo 15 bonbonů.
U: Zkuste to zmenšit jinak. Když víte, že dvě pětiny jsou moc a jedna pětina je málo…
Ž: Už to mám. Je to přesně jeden a půl pětiny.
U: Zkus to vyjádřit jinak, abys použil celá čísla.
Ž: Jsou to tři desetiny.
U: A jak to vychází se třemi desetinami? Propočítejte to.
…
Ž: To nejde.
U: Co nejde?
Ž: Vyšlo mi, že Eliška má devět bonbonů. Terezce jsem dala o třetinu míň, tedy šest. Dohromady mají 15 bonbonů, ale z toho nejde vzít polovinu ani čtvrtinu.
Ž: Tak dej Terezce o dvě třetiny míň. Potom budou mít dohromady dvanáct a to už jde rozdělit.
Ž: Ale Terezka bude mít ze všech nejmíň.
U: Zdá se, že měnit zadání se zlomky není tak snadné, aby úloha vycházela, jak chceme. Zkuste tedy vytvořit jednodušší úlohu se zlomky. Použijte první dvě věty ze zadání, ale upravte je. Představte si, že máte dvanáct bonbonů rozdělit mezi tři děti tak, aby dostaly 3, 4 a 5 bonbonů. Počty nemusí být v tomto pořadí. Až budete mít zadání úlohy napsané, dejte ji vyřešit spolužákovi v lavici.

Od řešení slovní úlohy se žáci dostali k jejímu tvoření. Rozbor řešené situace ukázal, že dělení celku na různě velké části vyjádřené zlomky nemusí být v některých případech snadné. Žáci vyzkoušeli různé varianty, ale k požadavku vyrovnaných počtů se nedopracovali. Proto učitel přistoupil k výraznému zjednodušení původní úlohy a zároveň žákům zadal počty, k nimiž má zadání nové úlohy vést, aby omezil počet možností. Žáci vytvořili některou ze šesti následujících variant:

Z bonboniéry se 12 bonbony snědla Eliška 1/4 bonbonů. Terezka snědla o 1/3 více než Eliška. Ondra dostal zbytek. (výsledné rozdělení bonbonů: E = 3, T = 4, O = 5)

Z bonboniéry se 12 bonbony snědla Eliška 1/4 bonbonů. Terezka snědla o 2/3 více než Eliška. Ondra dostal zbytek. (výsledné rozdělení bonbonů: E = 3, T = 5, O = 4)

Z bonboniéry se 12 bonbony snědla Eliška 1/3 bonbonů. Terezka snědla o 1/4 méně než Eliška. Ondra dostal zbytek. (výsledné rozdělení bonbonů: E = 4, T = 3, O = 5)

Z bonboniéry se 12 bonbony snědla Eliška 1/3 bonbonů. Terezka snědla o 1/4 více než Eliška. Ondra dostal zbytek. (výsledné rozdělení bonbonů: E = 4, T = 5, O = 3)

Z bonboniéry se 12 bonbony snědla Eliška 5/12 bonbonů. Terezka snědla o 1/5 méně než Eliška. Ondra dostal zbytek. (výsledné rozdělení bonbonů: E = 5, T = 4, O = 3)

Z bonboniéry se 12 bonbony snědla Eliška 5/12 bonbonů. Terezka snědla o 2/5 méně než Eliška. Ondra dostal zbytek. (výsledné rozdělení bonbonů: E = 5, T = 3, O = 4)