SLOVNÍ ÚLOHY S VÍCE POČETNÍMI OPERACEMI
Autor: Štěpánka Vondrášková, ZŠ Generála Janouška, Praha
Úvod
Slovní úlohy lze uchopit různými způsoby. Při jejich řešení ne všem žákům pomůže právě ten jeden, který jim učitel, učebnice nebo pracovní sešit nabízí. V této práci jsou uvedeny různé způsoby uchopení slovních úloh. V praxi se setkávám s případy, kdy si někteří žáci po přečtení slovní úlohy nevědí rady. Proto uvádím možné způsoby, jak si poradit se slovní úlohou. Možná, že i v některém ze způsobu řešení bude vaším pomocníkem.
Z pracovního sešitu a z učebnice pro 3. ročník nakladatelství Taktik jsou vybrány slovní úlohy s více početními operacemi. Obě úlohy jsou součástí pohádek. Některé dnešní děti neznají základní klasické pohádky, je jim tedy touto cestou umožněno seznámit se s těmito klasickými pohádkami nebo si je určitým způsobem připomenout a popřípadě je i dovyprávět.
V běžných třídách je široko spektrum žáků od slabých po nadané. Ukážeme si, jak obsáhnout toto spektrum.
Slabší žáci můžou pomocí manipulace s předměty rozebírat úlohu, vyučující je může navigovat a usměrňovat tak, aby úlohu vyřešili. Nadaní mohou samostatně pracovat až do dovyprávění pohádky.
Kapitola 1
Možné překážky při řešení matematické úlohy
Slovní úlohy jsou mnohdy dětem předkládány jako něco, co má svá pevná pravidla. Zápis daného formátu, tvorba matematické úlohy, řešení, výsledek matematické úlohy a závěr. Někdy právě toto může být pro některé určitou stopkou. Jak si poradit se slovní úlohou?
Důležité může být modelování reálné situace, kde dojdeme k výsledku matematické úlohy a k opětovnému návratu k reálné situaci v odpovědi matematické úlohy.
V závěru pracovního sešitu Hravá matematika pro 3. ročník jsou uvedeny úlohy s více početními operacemi. Tyto úlohy na sebe vzájemně navazují a jejich tématem je pohádka o Smolíčkovi. V poslední době se kantoři setkávají s případy, kdy se děti s klasickou pohádkou prakticky nesetkají, a zde je jim umožněno se prostřednictvím pohádky ponořit do světa matematiky a pohádky jako takové. Také slovní zásoba u některých žáků bývá chudší a řada běžných slov je jim cizí. Ukážeme si, jak si poradit i s tímto.

Převzatý příklad – citace z pracovního sešitu Hravá matematika pro 3.ročník: BALEJOVÁ, Renata, Martina HUBKOVÁ, Štěpánka VONDRÁŠKOVÁ, Zuzana ŠVIHLOVÁ a Ivona ŠPAČKOVÁ. Hravá matematika 3: pro 3. ročník ZŠ. 2. vydání. Praha: Taktik, 2021. ISBN 978-80-7563-143-5
U některých slovních úloh, které jsou uváděny v pracovních sešitech nebo učebnicích, je žákům předepsán mustr zápisu slovních úloh. I tady v tomto sešitě je tomu tak u prvních třech úloh. Dítě, a někdy i vyučující se tak mylně domnívá, že právě tato cesta zápisu je jedinou správnou. Je zde uváděno jen jako možný způsob řešení, ne však něco, co je nutné tak psát.
Jak se ukázalo, toto však může vést některé děti k zaražení, chtěly by úlohu řešit jinak. Dáme tedy prostor pro jejich vlastní kreativitu, a to je třeba jim říct. Nasměrovat je k tomu, že není jeden jediný způsob zápisu, stejně jako sestavení matematické úlohy a její řešení.
Kapitola 2
Jak na úlohu
- Dobré je, rozfázovat si úlohu na části. Vzít ji po větách a rozebrat si ji.
Při řešení některých matematických úloh dochází někteří žáci k nelogickému výsledku. Nakupují v obchodě, utratí peníze a zpět dostávají více peněz, než měli před nákupem. Rozbor slovní úlohy je proto dobrým pomocníkem, zvláště pro slabší čtenáře či slabší žáky.
- Ano, některým dětem mustr pomůže – můžeme je nechat pracovat s ním, ale netrvat na něm.
- Velmi dobře pomáhá manipulace s předměty, kdy dětem pomocí ní ukážeme, co znamenají pojmy „o něco více než“, „o něco méně než“, x krát více“, „x krát méně“, „dohromady“.
- Práce na interaktivní tabuli je velmi dobrý pomocník. Symboly reálných předmětů může dítě vybírat z nekonečného klonovače. Kolik potřebuje, tolikrát si vezme. Toto bývá pro děti poutavé.
- Pokud jsou uvedeny v úloze velká čísla, žáci si převedou tato čísla na menší. Manipulují s předměty menšího počtu, vyřeší matematickou úlohu a poté dosadí za malá čísla skutečná, velká čísla. Proč vůbec tato záměna? Některé děti se ve velkých číslech ztrácejí. Manipulace s menším počtem prvků a vrácení zpět do nižšího ročníku je tak upevní v jistotě, že matematickou úlohu podobného typu již zvládaly a zvládnou tak i tu s vyšším počtem prvků,
- Práce v terénu, v reálném prostředí. Zde žáci si utvrdí, co se naučili ve školních lavicích.
Při řešení úloh se můžeme setkat i se situacemi, kdy děti nebudou některá pro nás běžně užívaná slovíčka znát jejich význam. V takovém případě se osvědčí:
- a) Skupinová práce, kdy si děti vzájemně některá slovíčka vysvětlí. Žáci se lépe učí jeden od druhého.
- b) Řízená diskuze, kdy vyučující vyzve ostatní žáky k tomu, aby o daném slově diskutovali a dopracovali se k jeho významu.
Kapitola 3
Žákovské práce
V této kapitole si ukážeme některé žákovské práce. Ujistíte se, že nejsou všechny děti stejné a individualizace je potřebná i v přístupu ke slovním úlohám.

Obrázek 1: žákovská práce – Správné řešení, sestavení matematické úlohy a odpovědi. Samostatná práce (Vondrášková, 2022)
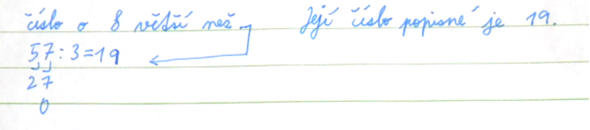
Obrázek 2: žákovská práce – chybný zápis (Vondrášková, 2022)
Tady došlo k chybnému zaznamenání ze strany dítěte, kdy si uvedlo podíl jako výsledek čísla popisného. Ve svém vlastním zápisu to má sice tak uvedeno, ale odpověď je jiná. Takový zápis je nefunkční.

Obrázek 3: žákovská práce – automatická početní operace (Vondrášková, 2022)
Správné řešení úlohy. Není vidět postup řešení, jak dítě přišlo na výpočet o osm větší. Jde o automatickou početní operaci, kterou provedlo ve své hlavě. Nelpíme na psané formě matematické úlohy a jejího výpočtu. Některé děti si vypočítají úlohu v hlavě a sestavení matematického zápisu je vlastně zdržuje, jak samy uvádějí v závěru této práce.

Obrázek 4: žákovská práce – složená matematická úloha (Vondrášková, 2022)
Jsou i tací žáci, co vytvoří jeden matematický zápis. Dítě sice vytvořilo jeden zápis, kde zjistilo podíl, uvědomilo si však, že nejde o finální výsledek a vytvořilo matematický zápis složený.
Konkrétně, jak si s úlohou poradit:
Při řešení této úlohy narazily děti na pojmy „podíl“, „číslo popisné“ – se kterými si nevěděly rady. Pokud pracovaly ve skupině, ve které se našel někdo, kdo této pojem znal, osvětlil ho ostatním a řešily společně matematickou úlohu dál.
Druhou z možností byla řízená diskuze, kdy se jim naznačilo, o co vlastně jde. V pozdějších vydáních tohoto sešitu se dokonce objevil i obrázek domu.

Obrázek 5: žákovská práce – potíže se slovní zásobou (Vondrášková, 2022)
Děti došly k závěru, co je podíl a číslo popisné. Dětsky uvedly: „Podíl je děleno.“
K zafixování tohoto pojmu se osvědčila obměna slov v úloze, kdy dětem, co již mají úlohu zvládnutou, nabídneme možnost jiné volby slov – číslo popisné je součin čísel, rozdíl čísel nebo součet čísel. Začnou v pojmech nabývat sebevědomí a s úlohou si pohrávají. Slabším dětem dáváme tak možnost vyřešit také úlohu samostatně, byť i manipulaci s předměty a dosazením menších čísel.
Kapitola 4
Manipulace s předměty
4.1 dosazení menšího počtu prvků
Ke snadnějšímu pochopení lze úlohu začít s dosazením menších čísel do úlohy a manipulovat s předměty. Pokud dítě samostatně nezvládne předepsanou úlohu, můžeme mu takto pomoci. V podstatě jde o vrácení se do nižšího ročníku. Dítě se ujistí, že podobnou úlohu již někdy dříve zvládalo. Manipulací s nižším počtem prvku je i snazší. Cílem je, aby žák přišel na postup řešení matematické úlohy.

Obrázek 6: žákovská práce – manipulace s menším počtem prvků (Vondrášková, 2022)
Obměna úlohy zní:
- Na kraji vesnice blízko lesa stojí chaloupka. Její číslo popisné je o 2 větší než podíl čísel 18 a 2. Jaké má chaloupka číslo popisné?
Děti si rozdělily hromádku 18 na 2 části. K jedné z nich přidaly 2 fazolky.
Vzhledem k tomu, že zde představuje číslo popisné pořadí, můžeme pracovat s číselnou osou. Některé děti však nemají plně orientaci čísla na číselné ose. Potřebovalo manipulaci s malými čísly, které si poté převedlo na daná čísla z úlohy.
Tato úloha je netypická, triková. Proč triková? U čísla chaloupky jde o pořadí chaloupky, ne o počet chaloupek na mýtině. Dítě, které má určité specifické problémy, zde získalo při manipulaci s fazolemi představu o tom, že je zde určité množství o něco větší než jiné. S číslem pracuje jako s množinou prvků. Manipulace s menším počtem fazolek mu byla nápomocna k vyřešení matematické úlohy. Poznalo, co to znamená podíl. S číslem se začaly dělat triky. Číslo mělo funkci symbolu, značilo pořadí a najednou se s ním dělaly triky. Vytvářel se podíl, který byl o něco větší. Tyto triky nemají nic společného s kontextem dané slovní úlohy. Při řešení této úlohy se dítě již musí orientovat v matematické symbolice. Vědět nebo si připomenout, co je to podíl. Na této slovní úloze se buduje představa, co je to podíl. Úloha se může gradovat na souřadná slova: součin, součet, rozdíl.
S úlohou si lépe poradily při použití malých čísel místo velkých. Po Vyřešení dosadily konkrétní čísla, která byla v úloze uvedena.
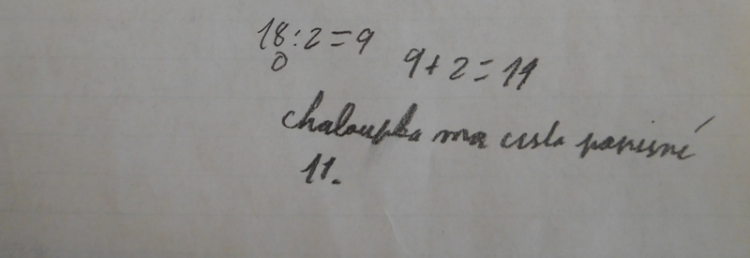
Obrázek 7: žákovská práce – dosazení menších čísel (Vondrášková, 2022)
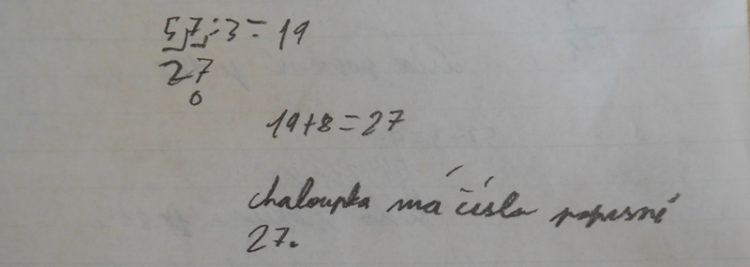
Obrázek 8: žákovská práce – dosazení skutečných čísel (Vondrášková, 2022)
Zápis úlohy toto dítě neuvedlo. Zdál se mu rušivý a v podstatě ho při řešení úlohy prý zdržoval.
4.2 použití číselné osy
Pokud budeme používat číselnou osu, můžeme úlohu přednést, jako myslím si číslo, které je o 8 větší než podíl čísel 57 a 9.
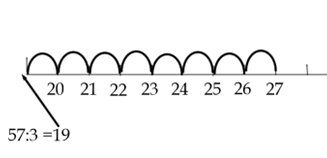
Obrázek 9: použití číselné osy (Vondrášková, 2022)
4.3 obměny matematické úlohy pro zdatnější žáky
Obměny úlohy pro zdatnější žáky, zatímco se slabší potýkají s danou slovní úlohou:
Na kraji vesnice blízko lesa stojí chaloupka. Její číslo popisné je o 18 větší než součin čísel 57 a 3. Jaké má chaloupka číslo popisné?
Na kraji vesnice blízko lesa stojí chaloupka. Její číslo popisné je o 26 větší než rozdíl čísel 57 a 3. Jaké má chaloupka číslo popisné?
Obrázek 10: žákovská práce (Vondrášková, 2022)
Tímto způsobem si děti připomenou pojmy a snadno řeší úlohy. Jde o stejný mustr, ale s obměnou čísel. Uvědomí si, že pokud zvládnou úlohu s menším počtem prvků, je pro ně pak snazší vyřešit ji s velkými čísly.
4.4 Slovní úloha s použitím interaktivní tabule
Rozebrat úlohu si mohou žáci i na interaktivní tabuli pomocí nekonečného klonovače a při práci ve skupinkách. Žáci se od sebe vzájemně učí a radí si.
https://www.youtube.com/watch?v=9pzEo2rU5Pw
Zdroj : https://zsgenjanouska.cz/wp-content/uploads/2022/05/Skolacek-6-2022.pdf s 21

Obrázek 11: použití mobilních přístrojů ve skupinkách(Vondrášková, 2022)
4.5 Práce v terénu
Práce v terénu –
Žáci měli sami nakoupit v obchodě a vejít se do určité částky peněz. Matematická slovní úloha se jim tak stala reálnou. Viděli, že obnos, který utrácí se nákupem nenavyšuje, spíše se zmenšuje. Vyučující sledoval žáky při nakupování. Před placením došlo ke kontrole, kdy vysvětlili vyučujícímu své postupy řešení.
Zajímavé bylo, že v rozhodné chvíli placení volili žáci spíše samoobslužnou pokladu než u pokladní. Došlo i k případu, kdy si žák peníze zapomněl. V tomto případě viděl, že mu pokladní částku neodpustí či neodloží na jiný den. Toto se mi zdálo výchovné a poučné pro všechny žáky. Někteří z žáků často zapomínají plnit své školní povinnosti a myslí si, že jim toto vždy bez následků nějak projde. Poznámka, ani snížená známka jim není motivací ke zlepšení.
Nákup v obchodním domě. Zdroj: https://zsgenjanouska.cz/wp-content/uploads/2022/03/Skolacek-5.pdf s 19

Obrázek 12: řešení slovní úlohy v reálu (Vondrášková, 2022)
Při řešení slovních úloh je lépe začínat nejdříve činnostními modely, vizuálními a pak teprve symbolikou. Dítě je třeba dát prostor dopracovat se k samotnému řešení úlohy.
Kapitola 5
Manipulace s předměty
V učebnici Hravá matematika pro 3. ročník, nakladatelství TAKTIK, je dětem předložena pohádka „Perníková chaloupka, aneb v pohádkách je možné vše.“
- Na kraji lesa v malé chaloupce bydleli tatínek, maminka a 2 děti. Tatínek pracoval v lese jako dřevorubec. Ve své dílničce měl uschovanou motorovou pilu, která měla 64 zubů. Když šel do lesa na dříví, vzal si s sebou ke své pile ještě 3 náhradní řetězy se stejným počtem zubů. Kolik zubů měly všechny 4 řetězy dohromady? Zaokrouhli počet zubů na stovky.
V učebnici již není dán dětem mustr zápisu. Děti se cítí volné ve způsobu řešení.
Některým slouží k pochopení úlohy manipulace s předměty ve spojení s menším počtem prvků.
5.1 Použití vlastního zápisu
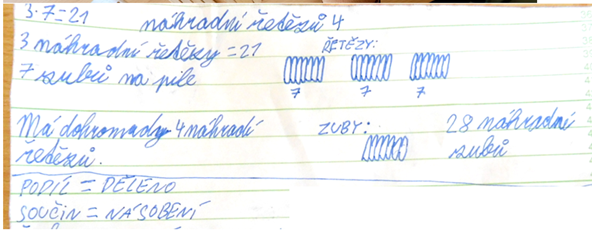
Obrázek 13: žákovská práce – vlastní zápis (Vondrášková, 2022)
Tady si úlohu rozebralo dítě, které má jinak problémy s uchopením úlohy. Úlohu si vypracovalo manuálně na menším počtu zubů. Tady názorně vidíme, že pro toto dítě je brzdou právě ten daný zápis.

Obrázek 14: žákovská práce – manipulace s fazolemi (Vondrášková, 2022)
 Obrázek 15: žákovská práce – manipulace s dřívky (Vondrášková, 2022)
Obrázek 15: žákovská práce – manipulace s dřívky (Vondrášková, 2022)
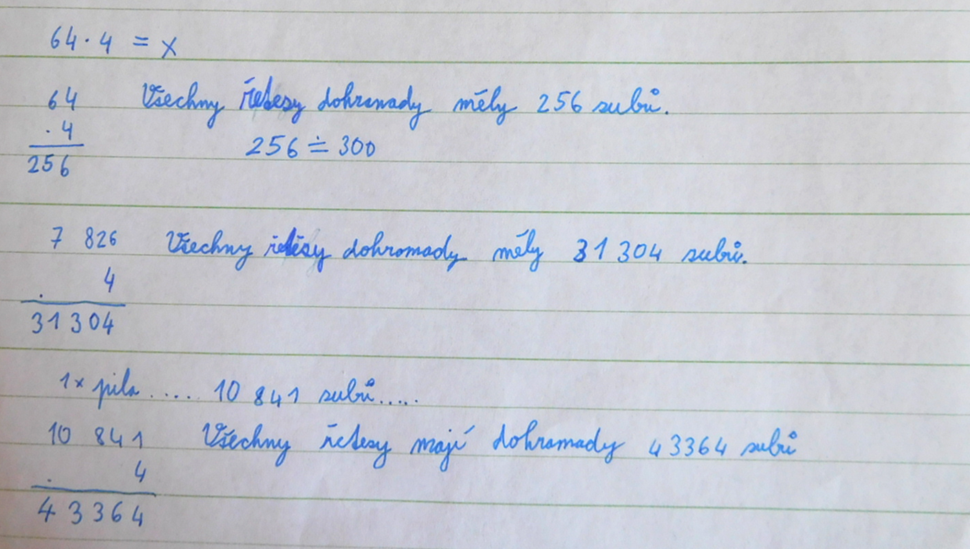
Obrázek 16: žákovská práce – přechod od malého počtu prvků ke skutečně uvedenému (Vondrášková, 2022)
Od malého počtu můžeme pro zdatnější žáky přecházet do jiného počtu zubů na pile. Mohou si procvičovat obměny úloh a procvičovat si nezávisle na slovní úloze násobení. Některé děti by mohlo napadnout, zda by pila mohla mít tolik zubů? Pokud takový dotaz podají, je vidět, že nad úlohou uvažují a nejde u nich jen o dosazování určitého počtu prvků do slovní úlohy. Pak můžeme takové žáky vést k tomu, aby podobnou úlohu vytvořili sami.
- Děti chtěly tatínka doprovodit. Vzaly si s sebou hrnečky na jahody. Mařenka nasbírala 226 jahod, ale 169 jich stačila sníst. Jeníček byl rychlejší. Nasbíral dvakrát více jahod než Mařenka. Dostal ale velký hlad a snědl z hrnečku 306 jahod. Kolik jahod celkem dětem v hrnečcích
Zůstalo?

Obrázek 17: žákovská práce – množiny (Vondrášková, 2022)
Názorně lze tento příklad rozkreslit s menším počtem prvků jako dvě množiny, kdy z každé ubereme určité množství prvků.
Následně dosadíme za menší čísla skutečná čísla, která jsou uvedena ve slovní úloze.
Dítě, které má běžně problémy s řešením slovní úlohy, úlohu vypočítalo. Dopustilo se chyby pouze v záměně čísla 236 místo 226. Jsou zde patrné stopy specifické poruchy učení. Jinak si s úlohou, po následné manipulaci s fazolemi, vědělo rady.

Obrázek 18: žákovská práce – žáci se SPU (Vondrášková, 2022)

Obrázek 19: žákovská práce – použití neznámé (Vondrášková, 2022)
Tady použilo dítě neznámou x, která je v matematické úloze nefunkční. Je zde brána jen formálně jako neznámá pro něj. Není brána jako neznámá v rovnici. Tento zápis s uvedením nějakého písmene či otazníku se ve školách často objevuje. Samotné dítě však toto nepotřebuje, jak je patrné ze zpětné vazby od žáků samotných či dle zápisu, které některé děti uváděly (na předešlé vyřešené matematické úloza). Některé děti jsou zvyklé psát x, y, ale je to vlastně zástup otazníku, něco, co neví. Dál s tím dítě tady již nepracuje.
Ve třídách běžně zažíváme děti, které si s úlohou vědí rady a děti, které potřebují určité postrčení. Dětem, které jsou rychlejší, dáme úlohy navíc, děti, které potřebují pomoc, necháme pracovat svým tempem, dokud úlohu nevyřeší.
Závěr
Zpětná vazba od žáků:

Obrázek 20: žákovská práce – zpětná vazba (Vondrášková, 2022)
Použitá literatura:
- BALEJOVÁ, Renata, Martina HUBKOVÁ, Štěpánka VONDRÁŠKOVÁ a Zuzana ŠVIHLOVÁ. Hravá matematika 3: pro 3. ročník ZŠ. Praha: Taktik, 2016. ISBN 978-80-87881-71-2.
- BALEJOVÁ, Renata, Martina HUBKOVÁ, Štěpánka VONDRÁŠKOVÁ a Zuzana ŠVIHLOVÁ. Hravá matematika 3: pro 3. ročník ZŠ. Praha: Taktik, 2016. ISBN isbn:978-80-87881-69-9
